SGD: unexpected parameters evolution during model training

1

Hi,

I have a very basic code to train a linear regression model. The code seems to work and it reacts as expected to the modifications of the learning rate. However I have noticed that I do not understand the evolution of the model’s parameters during the training.

Here is the code I use:

import pandas as pd
import torch

torch.manual_seed(42)

# generate some sample data
X = torch.rand(100, 1)
y = 2 * X + 1

# initialize model, loss and optimizer
model = torch.nn.Linear(1, 1)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

# train the model
num_epochs = 100

stats_params = {"weight": [model.weight.item()], "bias": [model.bias.item()]}

for epoch in range(num_epochs):
    # Forward pass
    outputs = model(X)
    loss = criterion(outputs, y)

    # Backward pass and optimization
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # store model's parameters
    stats_params["weight"].append(model.weight.item())
    stats_params["bias"].append(model.bias.item())

pd.DataFrame(stats_params).plot()

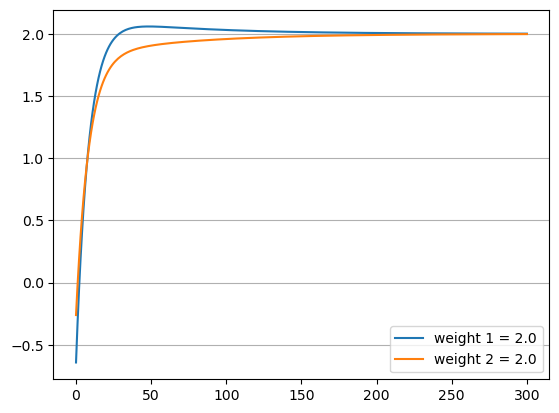
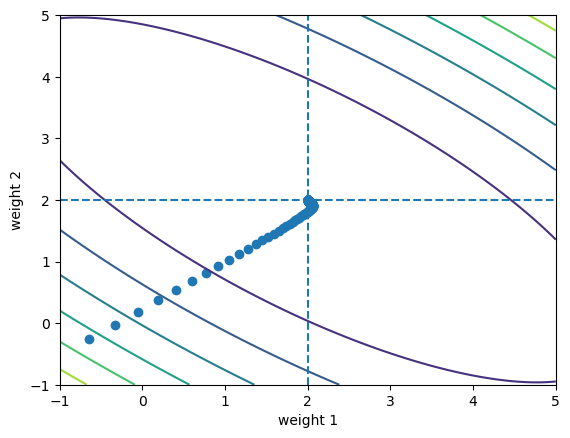
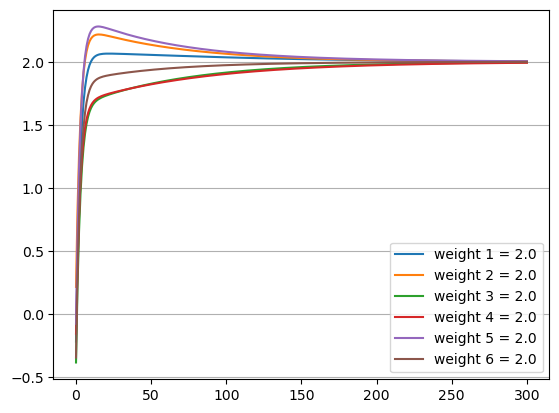
And here is the plot of the model’s parametrs evolution during the training:

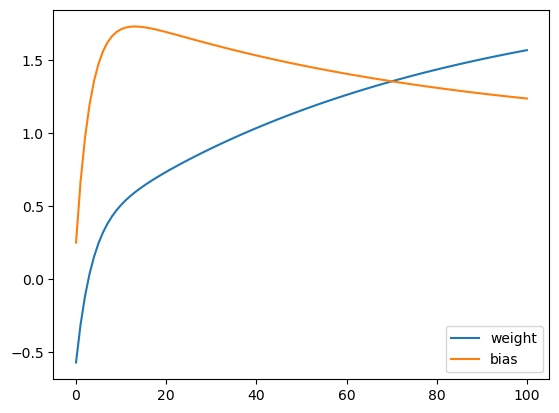
output

Given that the initial value of bias is below its true value 1, I would expect that in the process of model training it should monotonically increase and asymptotically tend towards the true value. As you can see, this is not what happens.

So is there an error in my code or is this evolution of the model’s parameters expected?

2

Until your weights get approximately in range they need to be, the bias will tend to be more chaotic. This is because weights are multiplied while the bias is added. So the weights are more dominant in the model outputs than the bias.

One way to think about this is considering a simple linear function:

f(x) = ax + b

Plug that into a graphing calculator. Now, let’s suppose you can only change a and b in discrete steps. Recall that a is the slope and b is the y-intercept. You might move the y-intercept closer, but find that changing the slope moves it away again.

So the slope is more important to get correct first because it scales as a multiple, while the bias only scales additively.

3

Thank you for your reply!

I understand what you mean, but I don’t agree with this explanation. In the case we are considering the model’s loss as a function of the model’s parameters is a simple quadratic surface, so the SGD optimizer should smoothly move the model’s parameters towards the optimum, provided that the learning rate is not too high.

Here is an updated example with a linear model without bias and with two weights, both equal to 2:

import matplotlib.pyplot as plt
import pandas as pd
import torch

torch.manual_seed(42)

# generate some sample data
n_features = 2
X = torch.rand(100, n_features)
true_weights = torch.full((n_features, ), 2.)
y = torch.matmul(X, true_weights).reshape(-1, 1)

# initialize model, loss and optimizer
model = torch.nn.Linear(n_features, 1, bias=False)
criterion = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.1)

# train the model
num_epochs = 300

def get_model_params(model):
    """Extract model params"""
    return torch.cat([param.data.squeeze().reshape(1, -1) for param in model.parameters()], dim=1)

stats_params = [get_model_params(model)]

for epoch in range(num_epochs):
    # Forward pass
    outputs = model(X)
    loss = criterion(outputs, y)

    # Backward pass and optimization
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    # store model's parameters
    stats_params.append(get_model_params(model))

stats_params = pd.DataFrame(torch.cat(stats_params).detach().numpy(), columns=[f"weight {i} = {w}" for i, w in enumerate(true_weights, 1)])

stats_params.plot()
plt.grid(axis="y")

The evolution of the model weights:
output

Once again, one of them overshoots the optimum and this is at complete odds with my understanding of the gradient descent.

The trajectory of the model’s parameters during optimization, also very strange for me:
output

This is what happens when we have more than two parameters (the model is still without bias and all weights are equal to 2) - half of the weights overshoot the optimum:
output

Note that in all cases the optimization finally converges to the true parameters and we get a correct model. However, I am puzzled by the behaviour of the optimizer and suspect an error in my code.

4

When I mentioned f(x) = ax + b, I was referring to your original code, whereas a is the weight, b is the bias and x is the input.

image
image806×177 9.3 KB

That is what a linear layer simplifies to in the case of 1 input and 1 output with bias=True. How the weight and bias converge is different, and that is what your original post demonstrated.

Additionally, some overshooting is to be expected when you have more than 1 weight as they are interdependent. If we could from the loss, alone, know both the relative angle and the magnitude of where the minimum is in relation to the current weights, we would not need to iterate. Just one run of the data and we could determine the optimum weights exactly. However, gradient descent only determines the magnitude and the slope. Thus it’s typically not traversed in a straight line.

5

Oh, that’s true. I haven’t revisited multivariate calculus for a long time and was stuck with a wrong picture that a general quadratic surface has gradient pointing towards its minimum. Now everything has come into the order.

Thank’s for your replies!

1 Like