Sigmoid + BCELoss not similar to BCEwithLogitsLOSS?

autograd
1

hello everyone ,
I’m coding the dropout as a variational inference as [ Gal et al 2016 ] explain it

I have a problem regarding “BCE With Logits Loss”

My simple neural net is

    def __init__(self, hidden_size, input_size=1, dropout_p=0.25 ):
        super().__init__()
        self.dropout_p = dropout_p
        
        self.hidden1 = nn.Linear(input_size,hidden_size)
        self.relu    = nn.ReLU()
        self.output  = nn.Linear(hidden_size,1)

    def forward(self, x):
        x = self.relu(self.hidden1(x))
        x = F.dropout(x,p=self.dropout_p)
        x = self.output(x)
        x = torch.sigmoid(x)
        return x

bnn = MLP(hidden_size=20,input_size=2)
bnn.train()
criterion = nn.BCELoss()
optimizer_bnn = torch.optim.SGD(bnn.parameters(), lr=0.01, momentum=0.90, nesterov=True, weight_decay=1e-6)

my training loop

torch.manual_seed(7)

fig, ax = plt.subplots(figsize=(7,7))
num_epochs=200

# To Do here

#########################  classical Gradient training loop ################################# 
for epoch in range(num_epochs):
    for (X,Y) in train_dataloader:  
            # Forward pass
            outputs = bnn(X.float())
            loss = criterion(outputs.float().reshape(-1), Y.float())

            # Backward and optimize
            optimizer_bnn.zero_grad()
            loss.backward()
            optimizer_bnn.step()
            
    # For plotting and showing learning process at each epoch, uncomment line below
    if (epoch+1)%10==0:
        plot_decision_boundary( bnn, X, Y, epoch, ((outputs.squeeze()>=0.5) == Y).float().mean(), 
                                nbh=4, model_type='mcdropout')
##############################################################################################



print('Finished Training')

My plot function

# Useful function: plot and show learning process in classification
def plot_decision_boundary(model, X, Y, epoch, accuracy, model_type='classic', samples=100, nbh=2, cmap='RdBu'):    
    h = 0.02*nbh
    x_min, x_max = X[:,0].min() - 10*h, X[:,0].max() + 10*h
    y_min, y_max = X[:,1].min() - 10*h, X[:,1].max() + 10*h
    xx, yy = np.meshgrid(np.arange(x_min*2, x_max*2, h),
                         np.arange(y_min*2, y_max*2, h))
    
    test_tensor = torch.from_numpy(np.c_[xx.ravel(), yy.ravel()]).float()
    if model_type=='classic':
        model.eval()
        pred = model(test_tensor)
    elif model_type=='svi':
        pred = model.forward(test_tensor, n_samples=samples).mean(0)
    elif model_type=='mcdropout':
        model.eval()
        model.training = True
        outputs = torch.zeros(samples, test_tensor.shape[0], 1)
        for i in range(samples):
            outputs[i] = model(test_tensor)
        pred = outputs.mean(0).squeeze()
    Z = pred.reshape(xx.shape).detach().numpy()

    plt.cla()
    ax.set_title('Classification Analysis')
    ax.contourf(xx, yy, Z, cmap=cmap, alpha=0.25)
    ax.contour(xx, yy, Z, colors='k', linestyles=':', linewidths=0.7)
    ax.scatter(X[:,0], X[:,1], c=Y, cmap='Paired_r', edgecolors='k');
    ax.text(-4, -7, f'Epoch = {epoch+1}, Accuracy = {accuracy:.2%}', fontdict={'size': 12, 'fontweight': 'bold'})
    display.display(plt.gcf())
    display.clear_output(wait=True)

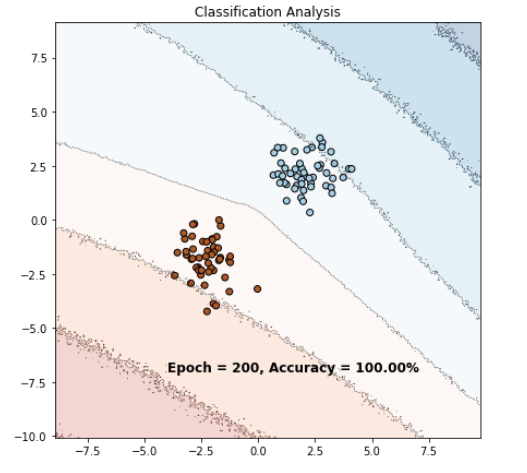
My problem is if I keep the sigmoid in the forward and use BCELoss I get this final result
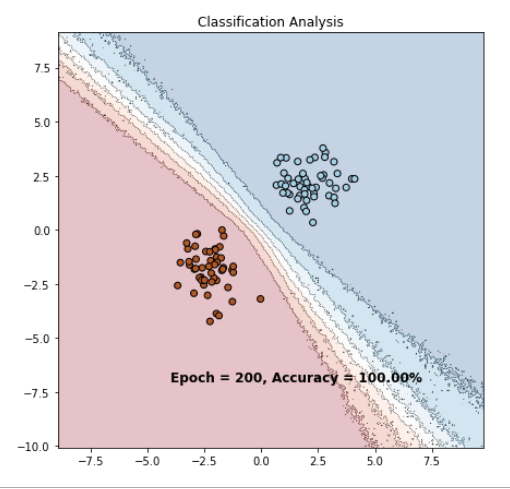
Screenshot from 2020-01-27 23-04-20
However if I change it without a sigmoid function and use BCEwithLogits I get this result
Screenshot from 2020-01-27 23-17-08

2

Hi Raouf!

I don’t follow in detail what you are doing, but be aware that
the output of a model with a final sigmoid() layer will, of
course, be different than the output of the analogous model
that lacks that layer.

With the sigmoid() layer your model returns probabilities.
Without the sigmoid() layer, your model returns “raw scores”
that are called logits.

Some comments appear in line, below.

Removing the x = torch.sigmoid(x) will, of course, change
the value x that your model returns.

The loss you calculate will be (more or less) the same if you
then use criterion = nn.BCEWithLogitsLoss() without
the sigmoid() layer, but the model’s output is different. This
difference – logits instead of probabilities – is compensated for
by using the different loss function.

Using outputs.squeeze()>=0.5 as your binary predictions
is appropriate when using the final sigmoid() layer. But unless
you change the logic for your prediction / accuracy calculation
when you remove the sigmoid() layer you will get different
(and incorrect) results.

When outputs are the logits you get without the sigmoid()
layer, you should use outputs.squeeze()>=0.0 to get your
binary predictions.

You plot Z. Z comes from preds, which comes from your model.
When you remove the sigmoid() from your model, you change
preds and Z, so your plots come out different because you are
plotting something different.

Best.

K. Frank

1 Like
4

My mistake was very obvious !
That’s the effect of coding at 2.00 am and copying my training loop from an above cell
Thanks a lot Sir