Hi PyTorch people,
I need to compute the Jacobian of a multi-variant vector-valued function w.r.t. its inputs. The problem I have is the dimension of the Jacobian is too large and it consumes a lot of GPU memory. What I’d like to do is to augment the current PyTorch implementation of torch.autograd.functional.jacobian and somehow return the Jacobian represented as a block sparse matrix. However, I run into an immediate problem that for every individual output element, I need to know whether or not an input element has participated in the computation. Normally, PyTorch gives us zero gradients if an input has not been used for computing a certain output element.
For example, if I run the following sample code,
import torch
from torch.autograd.functional import jacobian
def func(a0, a1, a2):
a0 = a0 * 0
a1 = a1 * 2
a2 = a2 * 4
e = torch.cat( (a0, a1, a2) )
return e
def func_single(g):
return func( g[:2], g[2:4], g[4:6] )
def test_jacobian_participation():
print() # Create an empty line.
a0 = torch.rand((2,), requires_grad=True)
a1 = torch.rand((2,), requires_grad=True)
a2 = torch.rand((2,), requires_grad=True)
g = torch.zeros((6,))
g[:2] = a0
g[2:4] = a1
g[4:6] = a2
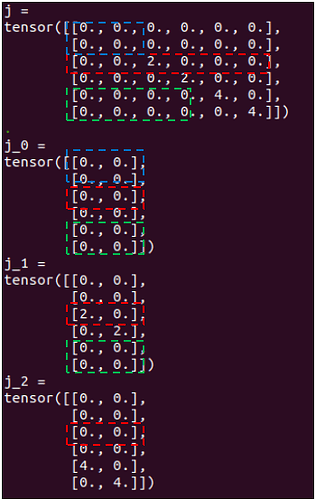
j = jacobian(func_single, g)
print(f'j = \n{j}')
def test_jacobian_participation_tuple():
print() # Create an empty line.
a0 = torch.rand((2,), requires_grad=True)
a1 = torch.rand((2,), requires_grad=True)
a2 = torch.rand((2,), requires_grad=True)
j_tuple = jacobian( func, (a0, a1, a2) )
for i, j in enumerate(j_tuple):
print(f'j_{i} = \n{j}')
if __name__ == '__main__':
test_jacobian_participation()
test_jacobian_participation_tuple()
I got the following in the terminal
During the call to the jacobian function, PyTorch does the computation in a row-based manner. That is the values for the Jacobian are computed row-by-row, as shown in the red dashed frames in the above figure. I am planning to modify this such that I can accumulate row results until I have enough rows for a single output object (such as 2 rows for a 2-vector representing the XY location of a 2D point, green and blue boxes in the above figure). One problem I have is that when I see one row or several rows of Jacobian values, how do I tell if a subset of zeros are there because of
- The associated input element does not participate in the computation of the output element (green boxes, should not go into the sparse block matrix).
- The associated input element participate in the computation but got multiplied by zero (blue boxes, should go into the sparse block matrix).
Any suggestions are appreciated! Thank you!