Specialized Normalization Running Slow in Pytorch

1

I have a tensor of shape z = (38, 38, 7, 7, 21) = (x_pos, y_pos, grid_i, grid_j, class_num), and I wish to normalize it according to the formula:
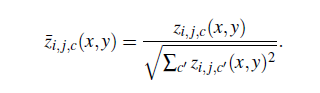
image

I have produced a working example of what I mean here, and the problem is that it is extremely slow, approximately 2-3 seconds for each grid entry (of which there are 49, so 49*3 seconds = 147 seconds, which is way too long, considering I need to do this with thousands of image feature maps).
Any optimizations or obvious problems very much appreciated. This is part of a Pytorch convolutional neural network architecture, so I am using torch tensors and tensor ops.

import torch
def normalizeScoreMap(score_map):
    for grid_i in range(7):
        for grid_j in range(7):
            for x in range(38):
                for y in range(38):
                    grid_sum = torch.tensor(0.0).cuda()
                    for class_num in range(21):
                        grid_sum += torch.pow(score_map[x][y][grid_i][grid_j][class_num], 2)
                    grid_normalizer = torch.sqrt(grid_sum)
                    for class_num in range(21):
                        score_map[x][y][grid_i][grid_j][class_num] /= grid_normalizer
    return score_map

random_score_map = torch.rand(38,38,7,7,21).cuda()
score_map = normalizeScoreMap(random_score_map)

Edit: For reference I have an i9-9900K CPU and a nvidia 2080 GPU, so my hardware is quite good. I would be willing to try multi-threading but I am looking for more obvious problems/optimizations.

2

This should work:

x = random_score_map.clone()
s = (x**2).sum(4, keepdims=True)
n = torch.sqrt(s)
x /= n

print(torch.allclose(x, score_map))
> True

Note that you should avoid for loops where possible and try to use vectorized code instead.