Speed difference in torch.einsum and torch.bmm when adding an axis

1

Hi,
When using self-attention, I found it’s common usage to use torch.einsum such as follows:

queries  =  torch.normal(0, 1, (b, h, q, d)).to('cuda') 
keys  =  torch.normal(0, 1, (b, h, q, d)).to('cuda')  # Because self-attention k == q
pre_softmax = torch.einsum("bhqd,bhkd->bhqk", queries, keys)

If my understanding is correct in that full self-attention example, we perform b*h*q*q operations.

If one wants to reduce the numbers of keys for each query to a fixed value k << q, then theoretically the number of operations reduces to b*h*q*k which should therefore reduce both time and memory complexity. Because one would have k separate keys for each query , the implementation using torch.einsum would look like the following:

queries  =  torch.normal(0, 1, (b, h, q, d)).to('cuda') 
keys  =  torch.normal(0, 1, (b, h, q, k, d)).to('cuda') 
pre_softmax = torch.einsum("bhqd,bhqkd->bhqk", queries, keys)

In practice, memory consumption does decrease by a factor q/k but not time complexity which becomes much larger as k grows.

On the other, if we simulate a scenario where the k keys are shared across all the q queries such that the code would look like the following :

queries  =  torch.normal(0, 1, (b, h, q, d)).to('cuda') 
keys  =  torch.normal(0, 1, (b, h, k, d)).to('cuda') 
pre_softmax = torch.einsum("bhqd,bhkd->bhqk", queries, keys)

We then obtain both linear improvement in time and memory as expected.

If we have a 1000 queries I plotted the following performance depending on k:

image
image819×545 32.2 KB

I was wondering what explained such difference in the implementation of einsum and I assume torch.bmm when the number of operations is the same? Is there a known way to get around this issue?

Thanks in advance !

Here is gist from a colab to replicate plot and with more example using also bmm directly.

2

It appears that some variant of this is a known issue Optimize torch.einsum · Issue #60295 · pytorch/pytorch (github.com) but I am not sure if anyone is actively working on it.

3

Hi, thanks for the answer @eqy!

I’ve tried to see if the issue was related by running additional experiments on the CPU to compare with the two suggested improvements.

From the following code, I believe we can conclude the issue isn’t related.

b, h, q, k, d = 8, 1, 1000, 100, 32
test_mat = torch.normal(0, 1, (b, h, q, d))
test_mat_u = test_mat.unsqueeze(-2) # (b, h, q, 1 ,d)
test_mat_q_k = test_mat_u.permute(0,1,3,2,4)[...,:k,:].tile((1, 1, q, 1, 1)) # (b, h, q, k, d)
test_mat_k = test_mat[...,:k,:] # (b, h, k, d)


print('### SEPERATE KEYS ###')

print("\n Timing contract('bhqd,bhqkd->bhqk', test_mat, test_mat_q_k, backend='torch') : 25.6M FLOPs")
%timeit contract("bhqd,bhqkd->bhqk", test_mat, test_mat_q_k, backend='torch')

print("\n Timing torch.einsum('bhqd,bhqkd->bhqk', test_mat, test_mat_q_k)  : 25.6M FLOPs")
%timeit torch.einsum("bhqd,bhqkd->bhqk", test_mat, test_mat_q_k)

print("\n Timing np.einsum('bhqd,bhqkd->bhqk',  test_mat.numpy(), test_mat_q_k.numpy())  : 25.6M FLOPs")
%timeit np.einsum("bhqd,bhqkd->bhqk", test_mat.numpy(), test_mat_q_k.numpy(), optimize='optimal')

print("\n Timing torch.matmul(test_mat_u, test_mat_q_k.transpose(-2,-1)).view(b,h,q,k) : 25.6M FLOPs")
%timeit torch.matmul(test_mat_u, test_mat_q_k.transpose(-2,-1)).view(b,h,q,k)


print('\n ### SHARED KEYS ###')

print("\n Timing contract('bhqd,bhkd->bhqk', test_mat, test_mat_k, backend='torch') : 25.6M FLOPs")
%timeit contract("bhqd,bhkd->bhqk", test_mat, test_mat_k, backend='torch')

print("\n Timing torch.einsum('bhqd,bhkd->bhqk', test_mat, test_mat_k)  : 25.6M FLOPs")
%timeit torch.einsum("bhqd,bhkd->bhqk", test_mat, test_mat_k)

print("\n Timing np.einsum('bhqd,bhkd->bhqk',  test_mat.numpy(), test_mat_k.numpy())  : 25.6M FLOPs")
%timeit np.einsum("bhqd,bhkd->bhqk", test_mat.numpy(), test_mat_k.numpy(), optimize='optimal')

print("\n  Timing torch.matmul(test_mat, test_mat_k.transpose(-2,-1)).view(b,h,q,k) : 25.6M FLOPs")
%timeit torch.matmul(test_mat, test_mat_k.transpose(-2,-1)).view(b,h,q,k)


print('\n ### ALL KEYS ###')

print("\n Timing torch.einsum('bhqd,bhkd->bhqk', test_mat, test_mat)  : 256M FLOPs")
%timeit torch.einsum("bhqd,bhkd->bhqk", test_mat, test_mat)

It returns:

### SEPERATE KEYS ###

 Timing contract('bhqd,bhqkd->bhqk', test_mat, test_mat_q_k, backend='torch') : 25.6M FLOPs
100 loops, best of 5: 16.4 ms per loop

 Timing torch.einsum('bhqd,bhqkd->bhqk', test_mat, test_mat_q_k)  : 25.6M FLOPs
100 loops, best of 5: 12.5 ms per loop

 Timing np.einsum('bhqd,bhqkd->bhqk',  test_mat.numpy(), test_mat_q_k.numpy())  : 25.6M FLOPs
100 loops, best of 5: 11.8 ms per loop

 Timing torch.matmul(test_mat_u, test_mat_q_k.transpose(-2,-1)).view(b,h,q,k) : 25.6M FLOPs
100 loops, best of 5: 12.4 ms per loop

 ### SHARED KEYS ###

 Timing contract('bhqd,bhkd->bhqk', test_mat, test_mat_k, backend='torch') : 25.6M FLOPs
1000 loops, best of 5: 1.34 ms per loop

 Timing torch.einsum('bhqd,bhkd->bhqk', test_mat, test_mat_k)  : 25.6M FLOPs
1000 loops, best of 5: 1.27 ms per loop

 Timing np.einsum('bhqd,bhkd->bhqk',  test_mat.numpy(), test_mat_k.numpy())  : 25.6M FLOPs
100 loops, best of 5: 13 ms per loop

  Timing torch.matmul(test_mat, test_mat_k.transpose(-2,-1)).view(b,h,q,k) : 25.6M FLOPs
1000 loops, best of 5: 1.27 ms per loop

 ### ALL KEYS ###

 Timing torch.einsum('bhqd,bhkd->bhqk', test_mat, test_mat)  : 256M FLOPs
100 loops, best of 5: 10.6 ms per loop

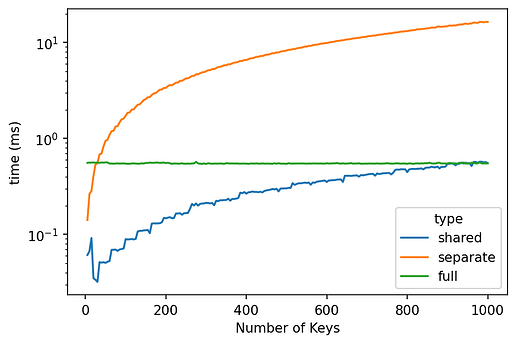
For a better contraction path, opt_einsum now supports torch. However, as shown above, using opt_einsum.contract doesn’t improve over torch.einsum.

For the second suggestion on discontiguous cases, I directly compared to np.einsum as it’s supposed t be handled in numpy. Unfortunately, similarly np.einsum doesn’t handle the additional dimension better. Moreover, np.einsum seems to implement the “shared” cases as the separate resulting in a similar run-time ( see above ).

If those two suggestions from the issue you gave seem to be a possible improvement for torch.einsum, this example seems to fall under neither specific case. Moreover, the issue seems to come from torch.matmul itself as it does show the same pattern in runtime, even though the FLOPs are similar between “shared” and “separate” keys cases.