Francisco Massa Luca Wehrstedt Ke Wen Will Constable
TL;DR: We avoided defining backwards for collectives for too long, because it was not urgent enough to push through some obscure stuff and align on an implementation. Now we’re seeing more usage of collectives and missing backwards support is becoming a serious problem.
Why Has This Taken So Long?
In short, because it’s harder than it sounds and nobody prioritized it enough. Autograd support was part of the ‘goals’ in the first Functional Collective RFC, but it was never a priority because in so many cases (FSDP, DDP, PP) there is no need for collective backwards, and for DTensor users, gradients are handled by DTensor itself. Worse, the gradient formula for a given collective is context-dependent, calling into question the validity of providing a ‘default’ backwards implementation in the first place (e.g. this comment).
I hope this post will serve first to demystify the issues around collective backwards. Second, I think there are some immediate actions we can take to improve things. And Third, we may need additional discussion on larger changes (e.g. RFCs), and we can refer back to this post as a ground truth.
What Are the Correct Backwards Formulas Anyway?
Let’s start by writing out the expected formulas from first principles, avoiding the implementation detail of multiple processes or comm libraries.
Example: naive_all_reduce
We can implement all_reduce as a function taking many input tensors and returning the reduced tensor multiple times as output.
def naive_all_reduce(inputs: list[torch.Tensor]) -> list[torch.Tensor]:
common_output = torch.sum(inputs)
return [common_output for _ in inputs]
Because we return multiple copies of the summed output, the gradients that come back from each ‘output path’ will be summed into the .grad field of ‘common_output’, before being passed back to each of the inputs. So this means our backwards pass is essentially another sum allreduce:
def naive_all_reduce_backward(d_outputs: list[torch.tensor]) -> list[torch.Tensor]:
accumulated_grad = torch.sum(d_outputs)
return [accumulated_grad for _ in d_outputs]
Using this framing, the mathematical formula for each operator should be unambiguous and indeed easy to verify just by using autograd on top of local torch operations.
One thing to call out, which will become important later: we are not making assumptions about our input/output tensors being related to one another in any way! This is the default assumption in pytorch, and indeed it is what you’d get if you ran torch.autograd on naive_all_reduce. But as we will see later, it is not what we actually want for many applications in distributed training.
Collectives
| Forward | Backward | Notes |
|---|---|---|
| gather | scatter | |
| scatter | gather | |
| reduce (avg, sum, premul_sum) | broadcast | Bitwise ops not supported for grad (band, bor, bxor) |
| reduce (max, min) | Identity (for max/min src) Scaled (for a tie) 0 (for others) | |
| reduce (product) | fwd_out / fwd_in * dout | |
| broadcast | reduce(sum) | |
| all_to_all | all_to_all | |
| all_reduce (avg, sum, premul_sum) | all_reduce(sum) | Common exception, e.g. megatron TP, see below; Bitwise ops not supported for grad (band, bor, bxor) |
| all_reduce (max, min) | all_reduce(sum) (for max/min src) 0 (for others) | |
| all_reduce (product) | fwd_out / fwd_in * allreduce(sum, dout) | |
| all_gather | reduce_scatter(sum) | |
| reduce_scatter | all_gather | |
| all_to_all | all_to_all |
Non-SPMD cases
We probably should not implement backwards automatically for non-spmd communication operations, even though the mathematical formula is trivial. This is because the ordering of operations during the backwards pass is critical to maintain correctness and avoid hangs, but we have no practical way of ensuring that we execute backwards graphs in a particular order. This can technically affect SPMD collectives too, but is particularly bad for Non-SPMD collectives.
| Forward | Backward |
|---|---|
| send | recv |
| recv | send |
Now that we have enumerated the backwards formulas, let’s see how people actually use collectives in practice.
These ‘mathematically correct’ backwards formulas for collectives are definitely useful in some cases. At least we have seen several examples recently: Tristan Rice used some for his Context parallelism prototype (code), and Ke Wen used some for his DeepSeek implementation (code).
Exceptions That Overrule The Rule
Let’s take a look at Tensor Parallelism as described in the original Megatron paper [1909.08053]. This is just one example, but the pattern it describes is extremely common in deep learning (moreso than the examples I could list above).
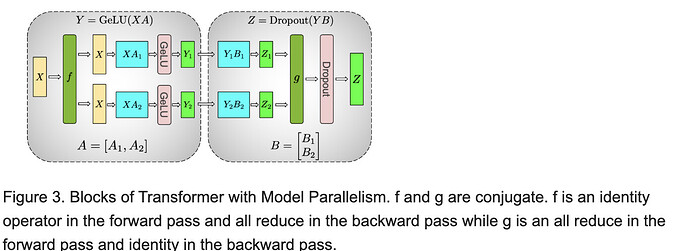
Figure 3. Blocks of Transformer with Model Parallelism. f and g are conjugate. f is an identity operator in the forward pass and all reduce in the backward pass while g is an all reduce in the forward pass and identity in the backward pass.
Communication operations f and g are introduced to perform a particular pattern of communication during forward and backwards that does not match any particular operator in our table above!
The whole point of f and g is to make a semantic leap. f takes a replicated tensor and makes it non-replicated. g merges non-replicated tensors back to replicated ones.
PyTorch DTensor has a similar concept. DTensors automatically track whether a tensor is a ‘Replica’ (e.g. X input to f) or ‘Partial’ (e.g. Z1 input to g), and offers APIs like ‘redistribute()’ to convert between these layouts.
Jax uses typing to tag values as ‘device-variant’ or ‘device-invariant’ [docs], and defines a set of operators that move values back and forth [docs]. pbroadcast is equivalent to f, while psum2 is equivalent to g. Note: psum itself also exists, and is equivalent to ‘all_reduce’, and the whole reason for introducing psum2 is to solve the issues outlined above.
Figure 4. Snippet from the table of operators introduced in JAX to transform between device-invariant and device-variant states.
So What Should We Do?
To recap, we can define mathematically pure gradient formulas for our collectives, but they don’t address some of the most common use cases. And we have a higher-level concept (call it replica vs partial, or device invariant vs variant) that we can make clearer and better supported in PyTorch.
Fix and Improve Collective APIs
-
[P0] We should patch the silent-correctness issue with functional collectives and C10d collectives by throwing an error in backwards ([C10D] Autograd Support for Collectives · Issue #152131 · pytorch/pytorch · GitHub
-
[P1] Implement mathematically pure backwards formulas for functional collectives and C10d collectives. (Note: naive backwards impl would be synchronous.) (([C10D] Autograd Support for Collectives · Issue #152131 · pytorch/pytorch · GitHub))
-
Deduplicate funcol, autograd_funcol, and nn.functional
-
[P2 / Optional] Improve eager backwards performance. (Alternative: rely on compile)
Explicitly Support the Device-Varying Case
Luca Wehrstedt and Francisco Massa point out that the existing DTensor internal helper method redistribute_local_tensor is very nearly what we’d need to offer a set of manual APIs that let users convert plain torch.Tensor between logically ‘replicated’ and ‘partial/device-varying’ states.
For users that don’t want to use DTensor for their whole program, we can still leverage its internals to offer a manual API that takes care of correctly transforming tensors between device-varying and device-invariant forms. In other words, we can offer the equivalent of f and g operations (as well as others described by JAX).
However, there are a few things we might need to harden about DTensor’s semantics. We’ll have to dive a little deeper here.
- Currently DTensor sharding rules are not as disciplined as they could be: A ‘replica’ tensor can directly be used as input to a matmul with a ‘shard’ input, while in a stricter sense we should force DTensor to convert the replica to a ‘partial’ first
- ‘redistribute_local_tensor’ has some questionable logic about skipping partial to replica conversion during backwards
I plan to look further into the explicit API and DTensor case, and update RFCs on pytorch accordingly. Hopefully this note clarifies the topic for folks, and if there is still something unclear or a mistake in the reasoning, please let me know!