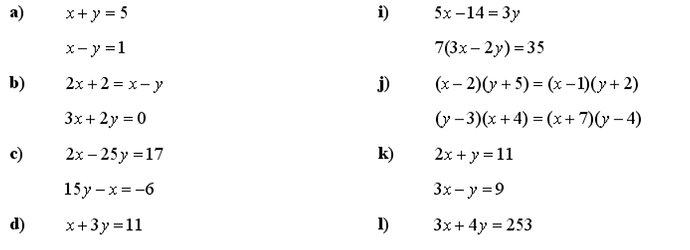System of linear equations, find x,y

1

Hi my question is pure mathematical problem, this is my code that finds x and y of System of linear equations. In this case, for this easy example equation:
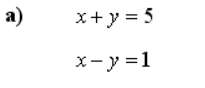
image

My question is- How can I transform equations like these to from Ax - b = 0 and then find x,y with Pytorch

image
image867×315 15.6 KB

Equations like these to from Ax - b = 0

x = torch.nn.Parameter (torch.zeros (2))
print(x.shape)
print(x)

def model(x):
    k = x[0] + x[1] -5
    z = x[0] - x[1] -1

    p =  torch.tensor([k, z])
    return k,z

optimizer = torch.optim.Adam([x], lr=0.1)

for i in range(500):
    target = torch.nn.Parameter (torch.zeros (2))

    k,z = model(x)
    loss = (0 - k)**2 + (0 - z)**2
    print(loss,loss)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()


print(x[0],x[1], "X Y ")
2

I think if you understand the meaning of Ax=b it’s straightforward
Basically you have to figure out A and b
for a)
A=(1,1)
(1,-1)
and b = (5,1)
in the example
b) 2x+2=x-y → x+y=-2
then
A = (1,1)
(3,2)
b=(-2,0)

Obtaining A and b allow you to rewrite the problem in a matricial way reusing the code.

1 Like
4

Thank you I understand now