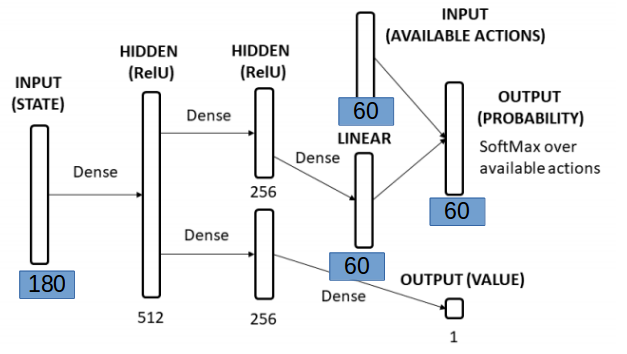
Hey Frank,
thanks for your very helpful and long answer and all your explanations. It would be cool if we could discuss more concrete on the code. I am not sure if I understood everything right. Here is the code based on your answer - would be nice if you can have a short look on it:
Using a constraint is a cool idea (unfortunately I am not sure how to incooperate that).
# tested with python 3.7.5
from torch.utils.data import Dataset
import ast
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from torch.autograd import Variable
# Links:
# https://www.kaggle.com/danieldagnino/training-a-classifier-with-pytorch
# https://discuss.pytorch.org/t/training-a-card-game-classifier/70625/2
class MyDataSet(Dataset):
'''A line in the dataset consists of
[bin_options+bin_on_table+bin_played]+[action_output+[round(bestq, 2)]]
Input: 180x1
Output: one-hot encoded 60x1
The bestq comes from the mcts estimation of how good the played action is
This values is currently not used.
'''
def __init__(self, data_root):
self.samples = []
with open(data_root,"r") as f:
self.samples = [ [ast.literal_eval(ast.literal_eval(elem)[0]), ast.literal_eval(ast.literal_eval(elem)[1])] for elem in f.read().split('\n') if elem]
print(len(self.samples)) # ca. 18000
def __len__(self):
return len(self.samples)
def __getitem__(self, idx):
# Function that returns one input and one output (label)
# as one dim output use:
# torch.Tensor(self.samples[idx][0]), torch.Tensor([self.samples[idx][1]].index(1))
return torch.Tensor(self.samples[idx][0]), torch.Tensor([self.samples[idx][1]])
class my_model(nn.Module):
'''
'''
def __init__(self, n_in=180, n_hidden=1, n_out=60):
super(my_model, self).__init__()
self.n_in = n_in
self.n_out = n_out
self.fc1 = nn.Linear(self.n_in, 120)
# TODO
# insert fully con layer here direclty connect
# hand with output
self.relu1 = nn.ReLU(inplace=True)
self.fc2 = nn.Linear(120, self.n_out)
def forward(self, x):
x = self.fc1(x)
x = self.relu1(x)
x = self.fc2(x)
return x
if __name__ == '__main__':
from torch.utils.data import DataLoader
my_data = MyDataSet('actions__.txt')
my_loader = DataLoader(my_data, batch_size=1, num_workers=0)
model = my_model()
criterium = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, weight_decay=1e-4)
# Taining.
loss_values = []
running_loss = 0.0
epoch = 0
for k, (data, target) in enumerate(my_loader):
data = Variable(data, requires_grad=False) # input
target = Variable(target.long(), requires_grad=False) # output
#squeeze the target here?!
# s your target has a channel dimension of 1, which is not needed using nn.CrossEntropyLoss or nn.NLLLoss.
#target = target.squeeze(1)
#TODO recast target one hot to single!
# Set gradient to 0.
optimizer.zero_grad()
# Feed forward.
pred = model(data)
print(pred.shape, target.shape) # torch.Size([1, 60]) torch.Size([1, 1, 61])
#ValueError: Expected input batch_size (1) to match target batch_size (61).
# Fails:
loss = criterium(pred, target.view(-1))
# Gradient calculation.
loss.backward()
# print statistics
running_loss += loss.item()
if k % 100 == 99: # print every 2000 mini-batches
print('[%d, %5d] loss: %.3f' %
(epoch + 1, k + 1, running_loss / 100 ))
loss_values.append(running_loss / 100 )
running_loss = 0.0
# Model weight modification based on the optimizer.
optimizer.step()
Further Notes:
I have currently 18786 batches -> I think I need more or?
One Batch (line) in actions__.txt looks like:
[’[0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]’, ‘[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, -9.96]’]