I have a very simple toy problem that is part of a greater research project. I am trying to prove that a single hidden-layer MLP can learn f(x) = x^2. We all know a shallow MLP can do this. The only caveat is that I am taking 64 different IID inputs, all drawn from a uniform distribution from [-5,+8]. Each of these 64 inputs gets squared, then we sum all 64 inputs to get our label y. As the inputs are IID, I am trying to show that they can all use a single input neuron into a single hidden unit MLP to learn x^2, since a common nonlinear operation is being performed on all inputs within the 64-dimensional input. Importantly, to de-bug, I have manually chosen parameters that are “close to optimal” for the network. This was by simply picking a linear combination of 14 ReLUs to build f(x)=x^2. These parameters are used for initialization.
Code with full working example (PyTorch Lightning but nothing specific within the problem to PTL):
import os
import torch
import pytorch_lightning as pl
from pytorch_lightning import LightningModule, Trainer
from torch import nn
import numpy as np
from torch.nn import functional as F
from torch.utils.data import DataLoader, TensorDataset
from torch.autograd import Variable
from pytorch_lightning.callbacks import ModelCheckpoint
from pytorch_lightning.loggers import WandbLogger
from pytorch_lightning.plugins import DDPPlugin
from pytorch_lightning.strategies.ddp import DDPStrategy
import torch.optim.lr_scheduler
os.environ['CUDA_LAUNCH_BLOCKING'] = "1"
torch.cuda.empty_cache()
def gen_data(in_N,t,low,high):
X = np.random.uniform(low,high,(t,in_N))
u = np.sum(X**2,axis=1)
return(X,u)
X,u = gen_data(64,100000,-5,8)
X_train = X[:90000,:]
X_train = torch.tensor(X_train)
X_validate = X[90000:,:]
X_validate = torch.tensor(X_validate)
Y_train = u[:90000]
Y_train = Y_train.reshape(90000,1)
Y_train = torch.tensor(Y_train)
Y_validate = u[90000:]
Y_validate = Y_validate.reshape(10000,1)
Y_validate = torch.tensor(Y_validate)
# Create dataset and dataloader for PyTorch
my_dataset_train = TensorDataset(X_train,Y_train)
my_dataset_val = TensorDataset(X_validate,Y_validate)
class x2(LightningModule):
def __init__(self):
super().__init__()
self.dropout_ff = torch.nn.Dropout(p=0.2)
self.fc1 = torch.nn.Linear(1,14)
self.fc2 = torch.nn.Linear(14,1)
self.activation1 = torch.nn.ReLU()
self.fc3 = torch.nn.Linear(64,1)
def forward(self,x):
x = x.float()
batch_sz = x.shape[0]
x = x.reshape(x.shape[0]*x.shape[1],1)
x = self.dropout_ff(x)
x = self.activation1(self.fc1(x))
x = self.dropout_ff(x)
x = self.fc2(x)
x = x.reshape(batch_sz,64)
x = self.dropout_ff(x)
u_pred = self.fc3(x)
return(u_pred)
def training_step(self, batch, batch_idx):
x, y = batch
y = y.float()
loss = torch.nn.MSELoss(reduction='mean')(self(x), y)
self.log("loss", loss, on_epoch=True, on_step=False, prog_bar=True, logger=True)
return(loss)
def validation_step(self, batch, batch_idx):
x, y = batch
y = y.float()
val_loss = torch.nn.MSELoss(reduction='mean')(self(x), y)
self.log("val_loss", val_loss, on_epoch=True, on_step=False, sync_dist=True, prog_bar=True, logger=True)
return(val_loss)
def predict_step(self, batch, batch_idx, dataloader_idx=0):
return(self(batch))
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=1e-4)
scheduler = torch.optim.lr_scheduler.StepLR(optimizer,step_size=20,gamma=0.9)
return([optimizer], [scheduler])
def main():
pl.seed_everything(350)
# Init our model
model = x2()
# Initialize weights at manually created ReLU to fit x^2 over domain of interest
model.fc1.weight.data = torch.tensor([[0.1],[-0.1],[0.5],[-0.5],[0.6],[-0.6],[1.5],[-1.5],[3.9],[-3.9],[2.0],[-2.0],[5.0],[1.0]])
model.fc1.bias.data = torch.tensor([0,0,-0.05,-0.05,-0.24,-0.24,-1.35,-1.35,-8.58,-8.58,-7.8,-7.8,-27.5,-7.1])
model.fc2.weight.data = torch.tensor([[1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0]])
model.fc2.bias.data = torch.tensor([0.01])
model.fc3.weight.data = torch.tensor([[1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,\
1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,1.0,\
1.0,1.0,1.0,1.0]])
model.fc3.bias.data = torch.tensor([-0.01])
# Init DataLoader from MNIST Dataset
train_loader = DataLoader(my_dataset_train, batch_size=100, shuffle = True, num_workers=24)
val_loader = DataLoader(my_dataset_val, batch_size=100, num_workers=24)
# Instantiate WandB loggers
wandb_logger = WandbLogger(name="x2", project='x2')
wandb_logger.watch(model, log="all", log_freq=10)
# Init ModelCheckpoint callback, monitoring "val_loss"
checkpoint_callback = ModelCheckpoint(dirpath='./',save_top_k=1,monitor="val_loss",mode='min',save_on_train_epoch_end=False,filename="x2",save_last=True)
# Initialize a trainer
trainer = Trainer(accelerator='gpu',strategy=DDPStrategy(find_unused_parameters=True),max_epochs=600,devices='auto',logger=wandb_logger,callbacks=[checkpoint_callback])
# Train the model
trainer.fit(model, train_dataloaders=train_loader, val_dataloaders=val_loader)
if __name__ == "__main__":
main()
The issue that I am running into is that despite the MSE decreasing during training (on the training set), the actual predictions are getting worse, as exemplified by a plot of the predicted Y vs true Y from the model at the beginning of training (parameters closer to manually initialized “optimal parameters”) vs the same plot for the model after training.
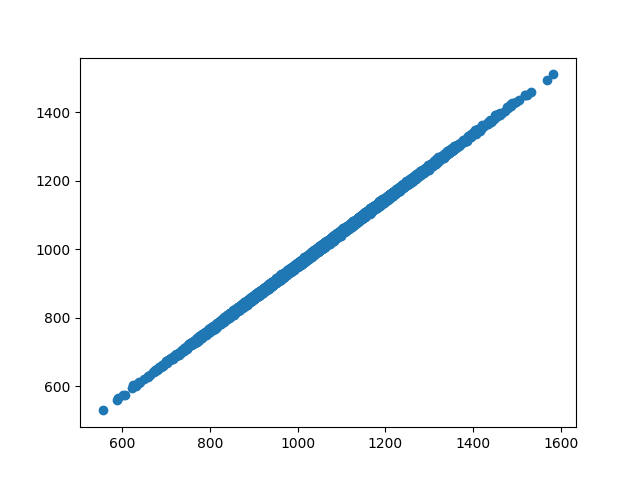
After 1 epoch, where training loss is at peak but parameters are closest to “optimal”, predicted Y vs true Y for training data:
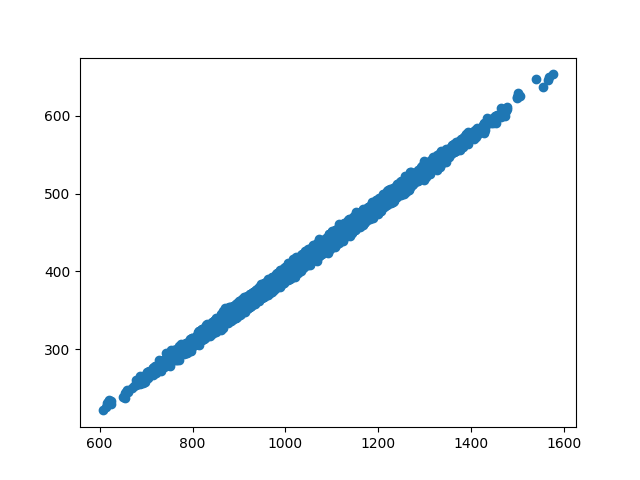
At the end of training, where training loss is a nadir but parameters have drifted from “optimal” initialized parameters, the predicted Y vs true Y for training data:
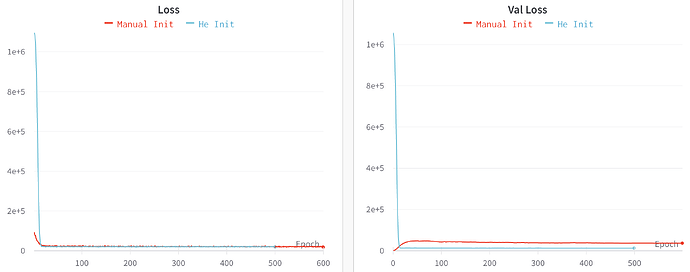
Interestingly, as this is toy, synthetic data, despite training and validation sets being IID, the loss dynamics during training look like this, with another model trained with He parameter initiation in blue:
None of this makes sense so I am trying to source ideas. I cannot come up with any reason as to how “learning” to minimize MSE is showing MSE decreasing during training, yet the MSE on the training set is clearly worse after training than before training (when parameters are close to “optimal” with manual init).