Hi there, relatively new pytorch user and new on forums, so hopefully I can make my issue clear below. Thank you in advance!
I am trying to train a model to learn, data point by data point (rather than batch) the mean and covariance matrix of multivariate normal distributions. This is a simple case, where the input data come from 2 multivariate distributions (2 “categories”), and I would like the model to learn these two distributions: first, initialize the model with 2 distributions, and on each trial, the distributions output their activations to a one-layer network to categorise it into one category or the other, and error is back propagated to learn the network weights, and the mean and the covariance matrices of the distributions (supervised learning). They should eventually look like the actual data distributions - learn that the data come from two distributions.
However, training the covariance matrix trial by trial means that sometimes the covariance matrix is a singular matrix. Is it possible to train the model so that the values in the covariance matrix only change to possible values?
See my working example below (apologies it’s a bit long, but it should work and plot something like I have posted here). If you make the learning rate of the covariance matrix (or the fc1) too fast, it leads to the error: RuntimeError: cholesky_cpu: For batch 1: U(2,2) is zero, singular U. Specifically in this case, if learning rate of the covariance matrix is 0.001 as I have it now, it errors. if you lower it to 0.0001, it works fine (‘lr_covmats’: .0001).
This is when it works relatively well (lr_covmats = 0.0001):
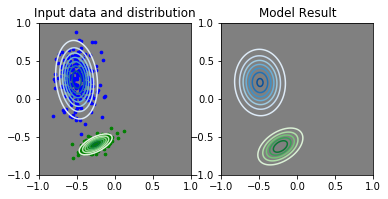
I’d like to be able to train this kind of model with a large range of parameters, so it would be annoying if this kind of error happens all the time.
Note:
- if you run the code below you should get an error. but if you make the learning rate slower you should get a plot of the input data and what the model learns at the end too
I’m using:
- pytorch 1.7.1.
- python 3.8
- Mac OS
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
import torch
import torch.nn as nn
import torch.optim as optim
# 2 distributions
mu1 = [-.5, .25]
var1 = [.0185, .065]
cov1 = -.005
mu2 = [-.25, -.6]
var2 = [.0125, .005]
cov2 = .005
# generate data points
npoints = 200
x1 = np.random.multivariate_normal(
[mu1[0], mu1[1]], [[var1[0], cov1], [cov1, var1[1]]], npoints)
x2 = np.random.multivariate_normal(
[mu2[0], mu2[1]], [[var2[0], cov2], [cov2, var2[1]]], npoints)
class DistrLearner(nn.Module):
def __init__(self, params=False, fitparams=False,
start_params=None):
super(DistrLearner, self).__init__()
self.n_dims = 2
self.nn_sizes = [2, 2] # only association ws
self.softmax = nn.Softmax(dim=0)
self.params = {
'lr_covmats': .00001, # .00001. w/ mom=0-.1. 00005 w/ mom=.3-.5
'lr_nn': .1, # .01, .1
'lr_mu': .002
}
# set starting mean / positions of the distributions
self.mu = torch.nn.Parameter(torch.tensor([[-.25, .05], [-.15, -.25]]))
# set starting covariance matrix
covmats = torch.eye(self.n_dims) * .02 # small for now - starting point
self.covmats = torch.nn.Parameter(covmats.repeat(2, 1, 1))
# one-layer net to categorise
self.fc1 = nn.Linear(2, self.nn_sizes[1], bias=False)
# set weights to zero
self.fc1.weight = (
torch.nn.Parameter(torch.zeros([self.nn_sizes[1],
2])))
def forward(self, x):
# mvn with centres specified by mu and cov mat covmats
mvn1 = torch.distributions.MultivariateNormal(self.mu, self.covmats)
# get activation of mvn by current data point, not log_pr
act = torch.exp(mvn1.log_prob(x))
# association weights / NN
out = self.fc1(act)
return out
def train(model, inputs, output, n_epochs, loss_type='cross_entropy',
shuffle=False):
criterion = nn.CrossEntropyLoss()
# buid up model params
p_fc1 = {'params': model.fc1.parameters()}
p_covmats = {'params': [model.covmats], 'lr': model.params['lr_covmats']}
p_mu = {'params': [model.mu],
'lr': model.params['lr_mu']}
params = [p_fc1, p_mu, p_covmats]
optimizer = optim.SGD(params, lr=model.params['lr_nn'], momentum=0.3)
model.train()
torch.manual_seed(5)
for epoch in range(n_epochs):
shuffle_ind = torch.randperm(len(inputs))
inputs_ = inputs[shuffle_ind]
output_ = output[shuffle_ind]
for x, target in zip(inputs_, output_):
# learn
optimizer.zero_grad()
out = model.forward(x)
loss = criterion(out.unsqueeze(0), target.unsqueeze(0)) # 1 trial by trial
loss.backward()
optimizer.step()
return model
# position of the datapoints
inputs = torch.cat([torch.tensor(x1, dtype=torch.float32),
torch.tensor(x2, dtype=torch.float32)])
# category the datapoint belongs to
output = torch.cat([torch.zeros(npoints, dtype=torch.long),
torch.ones(npoints, dtype=torch.long)])
n_epochs = 5
# initialize and run model
model = DistrLearner()
model = train(model, inputs, output, n_epochs, shuffle=True)
# plot data and results
x, y = np.mgrid[-1:1:.01, -1:1:.01]
pos = np.dstack((x, y))
fig1, ax1 = plt.subplots(1, 2)
# input data
rv1 = multivariate_normal([mu1[0], mu1[1]], [[var1[0], cov1], [cov1, var1[1]]])
rv2 = multivariate_normal([mu2[0], mu2[1]], [[var2[0], cov2], [cov2, var2[1]]])
ax1[0].contour(x, y, rv1.pdf(pos), cmap='Blues')
ax1[0].contour(x, y, rv2.pdf(pos), cmap='Greens')
ax1[0].scatter(x1[:, 0], x1[:, 1], c='blue', s=7)
ax1[0].scatter(x2[:, 0], x2[:, 1], c='green', s=7)
ax1[0].set_facecolor((.5, .5, .5))
ax1[0].set_xlim([-1, 1])
ax1[0].set_ylim([-1, 1])
ax1[0].set_title('Input data and distribution')
ax1[0].set_aspect('equal', adjustable='box')
# results
rv1 = multivariate_normal(model.mu[0].detach(), model.covmats[0].detach())
rv2 = multivariate_normal(model.mu[1].detach(), model.covmats[1].detach())
ax1[1].contour(x, y, rv1.pdf(pos), cmap='Blues')
ax1[1].contour(x, y, rv2.pdf(pos), cmap='Greens')
ax1[1].set_facecolor((.5, .5, .5))
ax1[1].set_xlim([-1, 1])
ax1[1].set_ylim([-1, 1])
ax1[1].set_title('Model Result')
ax1[1].set_aspect('equal', adjustable='box')