Trying to calculate gradient penalty with grad() detaches computational graph

1

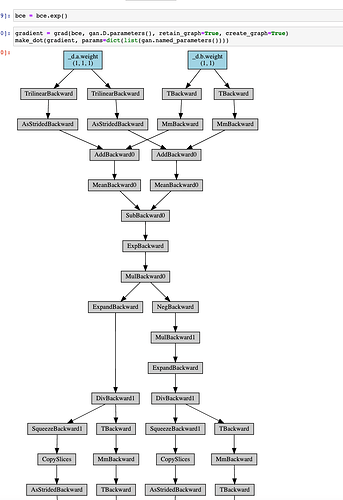
I have a very simple discriminator for a toy GAN problem where I’m trying to find the magnitude of the gradient in order to apply a penalty to the gradient. In order to do that, I need the gradient norm to be differentiable.

When I calculate the loss function for the generator I get the following computational graph:

# This code produces a tensor with a GradFn
bce = -1 * d_z.mean()

And then when I differentiate the loss with respect to the parameters I get a valid graph:

# This code produces a tensor with a GradFn
gradient = grad(bce, gan.G.parameters(), retain_graph=True, create_graph=True)

Here is the code for the generator:

class Linear(nn.Module):
    def __init__(self, in_features: int, out_features: int):
        super(Linear, self).__init__()
        self.W = nn.Linear(in_features, out_features)

    def forward(self, x: Tensor) -> Tensor:
        return self.W(x)

Now… when I do the same thing for the discriminator, it doesn’t work. The loss works fine:

# This code produces a tensor with a GradFn
d_x = gan.D(X)
d_z = gan.D(g_X.detach())
bce = d_z.mean() - d_x.mean()

But when I try to differentiate it again I get no graph:

Screen Shot 2020-10-20 at 8.51.22 PM
Screen Shot 2020-10-20 at 8.51.22 PM698×98 11 KB

And here is the code for the discriminator. As you can see, I’m only using building blocks from torch.nn so requires_grad should be true for everything:

class Quadratic(nn.Module):
    def __init__(self, in_features: int, out_features: int):
        super(Quadratic, self).__init__()
        self.a = nn.Bilinear(in_features, in_features, out_features, bias=False)
        self.b = nn.Linear(in_features, out_features, bias=False)

    def forward(self, x: Tensor) -> Tensor:
        return self.a(x, x) + self.b(x)

I’ve been trying to debug this all day, any help would be greatly appreciated!

2

Hi,

Do you set requires_grad afterwards for some reason on the params of gan.D ?
Are you sure that your function is twice differentiable with respect to your parameters (and non-zero) though?

What happens if for the sake of the experiment you do bce = bce.exp() to ensure the function is properly differentiable?

3

I’m using just nn.Linear() and nn.Bilinear() layers so it should be twice differentiable.

Well I’ll be damned, when I do that I get a proper graph:

Screen Shot 2020-10-21 at 11.28.15 AM
Screen Shot 2020-10-21 at 11.28.15 AM824×1198 75.5 KB

4

They are twice differentiable but at least for Linear, the second derivative is 0. And the autograd detects that the gradient is independent of the input and does not create graph for it.

5

Well that’s the thing… The equation for the generator is Ax + b, so if anything it should be the one not returning a gradient, but it does.

6

Unfortunately in the autograd, we don’t make a difference between “is independent” and “is 0”.
Also such gradient can be represented as:

  • A Tensor full of 0s
  • None (or undefined tensor on the c++ side)
  • An error if you use autograd.grad(..., allow_unused=False)

And the reason for this is that sometimes it will create a graph that produces only 0s and sometimes won’t create the graph at all.
The problem is that it is very hard to be always consistent here as we would like to never create the graph ideally, but we don’t want to have to do extra work either to know if we should create it or not.

7

I feel like there might be a miscommunication here. Ultimately, what I’m trying to do is get the 2-norm of the gradient (first derivative), and add it as a term to the overall loss function. While it is true that the generator is linear, I’ve worked the math out in closed form and the second derivative (Hessian) of the loss function with respect to the parameters is in fact non-zero. Once again, the generator returns a proper graph and the gradient is non-zero, as expected. The problem is the discriminator, which is bilinear and should have a non-zero hessian no matter what. Sorry if I’m not doing a good job of explaining.

8

But the example you showed takes the mean, not the 2 norm! That makes a big difference!

9

The mean is to aggregate the losses into a single value

10

Ho that is a different part of the code ok!
The thing is that if the autograd does not create the graph, that means that the gradient will just always be 0 based on what you computed.
Maybe you can share a full code sample that shows your problem?

11

Here is a self-contained example, but as you can see it actually works now! This confirms that there is a bug somewhere in my code. I’ll take a closer look and report back once I find it:

import torch as tr
from torch.autograd import grad

# Generate data, 1000 samples from a normal distribution
X = tr.normal(tr.ones(1000)).view(-1, 1)
Z = tr.normal(tr.zeros(1000)).view(-1, 1)

# Define the generator and discriminator
# Generator: Az + b
class G(tr.nn.Module):
    def __init__(self):
        super(G, self).__init__()
        self.Ab = tr.nn.Linear(1, 1)
    
    def forward(self, x):
        return self.Ab(x)

# Discriminator: x^T C x + d^T x
class D(tr.nn.Module):
    def __init__(self):
        super(D, self).__init__()
        self.C = tr.nn.Bilinear(1, 1, 1, bias=False)
        self.d = tr.nn.Linear(1, 1, bias=False)
    
    def forward(self, x):
        return self.C(x, x) + self.d(x)

g = G()
d = D()

# Test to make sure outputs are valid
print("Generator Test:", g(Z).mean())
print("Discriminator Test:", d(X).mean(), d(g(Z)).mean())

# Define loss:
generator_loss = -1 * d(g(Z)).mean()
discriminator_loss = d(g(Z)).mean() - d(X).mean()

# Test to make sure loss is differentiable
print("Generator Loss:", generator_loss)
print("Discriminator Loss:", discriminator_loss)

# Get gradient wrt parameters
generator_gradient = grad(generator_loss, g.parameters(), retain_graph=True, create_graph=True)
discriminator_gradient = grad(discriminator_loss, d.parameters(), retain_graph=True, create_graph=True)

# Both tensors should still have grad_fn
print("Generator Gradient:", generator_gradient)
print("Discriminator Gradient:", discriminator_gradient)

# Take 2-norm of gradient components
generator_norm = tr.norm(tr.cat([tr.flatten(i) for i in generator_gradient]))
discriminator_norm = tr.norm(tr.cat([tr.flatten(i) for i in discriminator_gradient]))

# Add to loss function, should STILL have grad_fn
final_gen_loss = generator_loss + generator_norm
final_disc_loss = discriminator_loss + discriminator_norm

print("Final Generator Loss:", final_gen_loss)
print("Final Discriminator Loss:", final_disc_loss)

Output:

Generator Test: tensor(-0.4425, grad_fn=<MeanBackward0>)
Discriminator Test: tensor(-0.9662, grad_fn=<MeanBackward0>) tensor(0.3021, grad_fn=<MeanBackward0>)
Generator Loss: tensor(-0.3021, grad_fn=<MulBackward0>)
Discriminator Loss: tensor(1.2683, grad_fn=<SubBackward0>)
Generator Gradient: (tensor([[-0.0995]], grad_fn=<TBackward>), tensor([0.6430], grad_fn=<ViewBackward>))
Discriminator Gradient: (tensor([[[-1.6031]]], grad_fn=<AddBackward0>), tensor([[-1.3847]], grad_fn=<AddBackward0>))
Final Generator Loss: tensor(0.3486, grad_fn=<AddBackward0>)
Final Discriminator Loss: tensor(3.3866, grad_fn=<AddBackward0>)
12

Also just for reference this is the paper I’m trying to implement

13

Ah, I figured it out! The problem is that I’m using the pytorch-lightning package, and it was freezing the weights of the other model for each step. On the discriminator step, the gradient norm is actually fully a function of the generator weights, so that was causing the problem. So it looks like I’ll have to probably write a custom optimizer to get the functionality I want.

1 Like