I have this Autoencoder Model which converges fine using the MSELoss (as I have numbers between -1 and 1).
class AutoEncoder(nn.Module):
def __init__(self):
super().__init__()
self._encoder = nn.Sequential(
nn.Conv2d(1, 16, 3, padding=1),
nn.LeakyReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(16, 4, 3, padding=1),
nn.LeakyReLU(),
nn.MaxPool2d(2, 2),
nn.Conv2d(4, 1, 3, padding=1),
nn.LeakyReLU(),
nn.MaxPool2d(2, 2),
nn.Flatten()
)
self._decoder = nn.Sequential(
Reshape(1, 2, 2),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ConvTranspose2d(1, 4, 3, padding=1),
nn.LeakyReLU(),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ConvTranspose2d(4, 16, 3, padding=1),
nn.LeakyReLU(),
nn.Upsample(scale_factor=2, mode='nearest'),
nn.ConvTranspose2d(16, 1, 3, padding=1),
nn.Tanh()
)
def forward(self, x):
_x = x
_x = self._encoder(_x)
_x = self._decoder(_x)
return _x
Here you can see the original and the reconstruction. I use a Gramian Angular Field to convert time series data into a 2d matrix and back.
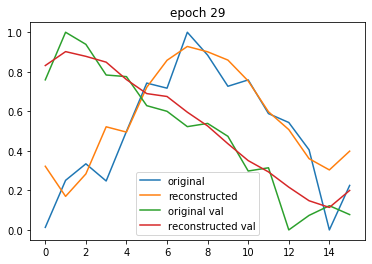
Now I would like to turn this into Variational Autoencoder but I can’t get it to converge any more.
# custom loss function used for training
class KLDivergence(nn.Module):
def __init__(self, criterion=nn.MSELoss()):
super().__init__()
self.criterion = criterion
def forward(self, y_hat, y):
y_hat, x, mu, logvar = y_hat
bce = self.criterion(y_hat, x).mean()
#bce = t.nn.functional.binary_cross_entropy(y_hat * 0.5 + 0.5, x * 0.5 + 0.5)
#bce = t.nn.functional.nll_loss(y_hat.view(y.shape[0], -1) + 1, x.view(y.shape[0], -1) + 1)
kld = -0.5 * t.sum(1 + logvar - mu.pow(2) - logvar.exp())
# kld /= x.shape[0] * x.shape[1]
return bce + kld
class VARAutoEncoder(AutoEncoder):
def __init__(self):
super().__init__()
self.mu = nn.Linear(4, 4)
self.sigma = nn.Linear(4, 4)
self.unpack = lambda x: x # nn.Linear(4, 4)
def forward(self, x):
mu, logvar = self._encode(x)
if self.training:
z = self._reparam(mu, logvar)
return self._decode(z), x, mu, logvar
else:
return self._decode(mu)
def _encode(self, x):
x = self._encoder(x)
return self.mu(x), self.sigma(x)
def _decode(self, x):
return self._decoder(self.unpack(x))
def _reparam(self, mu, logvar):
std = logvar.mul(0.5).exp_()
eps = Variable(std.data.new(std.size()).normal_())
return eps.mul(std).add_(mu)
As a new user I can only put one image into the post but both reconstructions are now just kind of a straight horizontal line. If I remove the kld term from the loss and only return the bce it reconstructs as nicely as before (I just doubt that the bottle neck follows a normal distribution then - right?).

