Unable to find minimum with optimizer

1

After being able to find the minimum value with scipy.optimize, I tried to implement the logic to find the optimal values with torch. When I tried to run the optimizer, it returned nan values.
This is the code that I used to find the minimum with scipy.optimize:

def get_pow_geometric(f, angle, power):
    return np.sign(f(angle))*np.abs(f(angle)) ** power

def get_distance(latent_params, p, a, epsilon, offset):
    eta, omega = latent_params
    p_x, p_y, p_z = p
    a_1, a_2, a_3 = a
    epsilon_1, epsilon_2 = epsilon
    x_0, y_0, z_0 = offset
    return np.sqrt((p_x - a_1*get_pow_geometric(np.cos, eta, epsilon_1)*get_pow_geometric(np.cos, omega, epsilon_2))**2 + (p_y - a_2*get_pow_geometric(np.cos, eta, epsilon_1)*get_pow_geometric(np.sin, omega, epsilon_2))**2 + (p_z - a_3*get_pow_geometric(np.sin, eta, epsilon_1))**2)

p = [0.9999999921748904, 0.9999999999999998, -2.0]
a_true = [1, 2, 3]
epsilon_true = [0.5, 0.5]
offset_true = [0, 0, 0]
optimization_result = optimize.minimize(get_distance, [0, 0], args=(p, a_true, epsilon_true, offset_true))
eta_optim, omega_optim = optimization_result.x

eta_optim and omega_optim values are -0.4562815152391673 and 0.07042550187811288 respectively; the distance is 0.0717705948348535

Then I tried to use the optimizer the following way:

p = torch.tensor([x2[0], y2[0], z2[0]])
epsilon_true = torch.tensor(epsilon_true)
a_true = torch.tensor(a_true)
offset_true = torch.tensor(offset_true)

def get_pow_geometric(f, angle, power):
    return torch.pow(torch.sign(f(angle))*torch.abs(f(angle)), power)

def get_distance2(p, a, epsilon, offset):
    p_x, p_y, p_z = p
    a_1, a_2, a_3 = a
    epsilon_1, epsilon_2 = epsilon
    x_0, y_0, z_0 = offset
    x = torch.tensor([.1, .1], requires_grad=True)
    optimizer = torch.optim.Adam([x], lr=0.0001)
    for i in range(30000):
        optimizer.zero_grad()
        d = torch.sqrt((p_x - a_1*get_pow_geometric(torch.cos, x[0], epsilon_1)*get_pow_geometric(torch.cos, x[1], epsilon_2))**2 + (p_y - a_2*get_pow_geometric(torch.cos, x[0], epsilon_1)*get_pow_geometric(torch.sin, x[1], epsilon_2))**2 + (p_z - a_3*get_pow_geometric(torch.sin, x[0], epsilon_1))**2)
        d.backward(retain_graph=True)
        optimizer.step()
        print(x, d)

While running get_distance2(p, a_true, epsilon_true, offset_true), I get

tensor([0.1000, 0.1000], requires_grad=True) tensor(2.9710, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.1000, 0.1000], requires_grad=True) tensor(2.9709, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.1000, 0.1000], requires_grad=True) tensor(2.9709, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.1000, 0.1000], requires_grad=True) tensor(2.9708, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.1000, 0.1000], requires_grad=True) tensor(2.9708, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.0999, 0.1001], requires_grad=True) tensor(2.9707, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.0999, 0.1001], requires_grad=True) tensor(2.9707, dtype=torch.float64, grad_fn=<SqrtBackward>)
tensor([0.0999, 0.1001], requires_grad=True) tensor(2.9706, dtype=torch.float64, grad_fn=<SqrtBackward>)
....
tensor([-3.7954e-05,  1.8102e-01], requires_grad=True) tensor(2.0163, dtype=torch.float64, grad_fn=<SqrtBackward>)
....
tensor([nan, nan], requires_grad=True) tensor(nan, dtype=torch.float64, grad_fn=<SqrtBackward>)
....

I would appreciate if anyone suggested how to fix the code in order to be able to get the same results as in the case of using scipy.optimize.

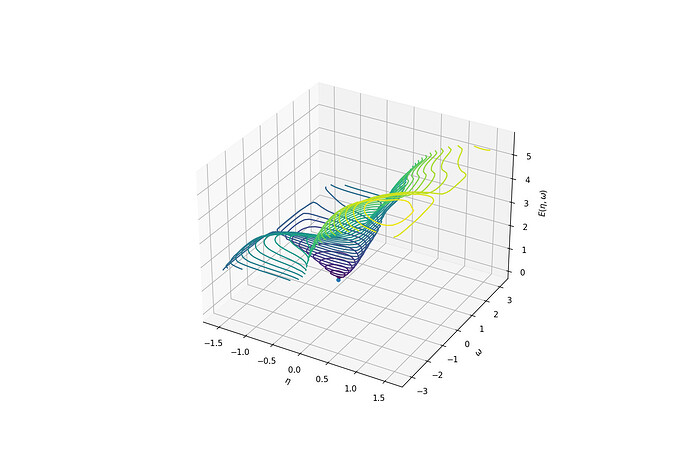
Below is the image, showing the function and the solution (obtained with scipy.optimize) - The function doesn’t seem to be that complex so I don’t know why the optimization fails.

download
download1320Ă—880 101 KB

2

Hi Niko!

Your pytorch code raises, in effect, f (angle) to a power, while your
numpy code raises np.abs (f (angle)) to a power. When f (angle)
is negative and power is fractional, your pytorch code will return nan.

(As an aside, pytorch also supports the “**” syntax for exponentiation.)

Consider:

>>> import torch
>>> torch.__version__
'1.7.1'
>>> def get_pow_geometric (f, angle, power):
...     return torch.pow (torch.sign (f (angle)) * torch.abs (f (angle)), power)
...
>>> def get_pow_geometric_B (f, angle, power):
...     return torch.sign (f (angle)) * torch.pow (torch.abs (f (angle)), power)
...
>>> def get_pow_geometric_C (f, angle, power):
...     return torch.sign (f (angle)) * torch.abs (f (angle))**power
...
>>> get_pow_geometric (torch.sin, torch.tensor ([1.0]), 0.5)
tensor([0.9173])
>>> get_pow_geometric (torch.sin, torch.tensor ([-1.0]), 0.5)
tensor([nan])
>>> get_pow_geometric_B (torch.sin, torch.tensor ([-1.0]), 0.5)
tensor([-0.9173])
>>> get_pow_geometric_C (torch.sin, torch.tensor ([-1.0]), 0.5)
tensor([-0.9173])

Best.

K. Frank

1 Like