Hello together,
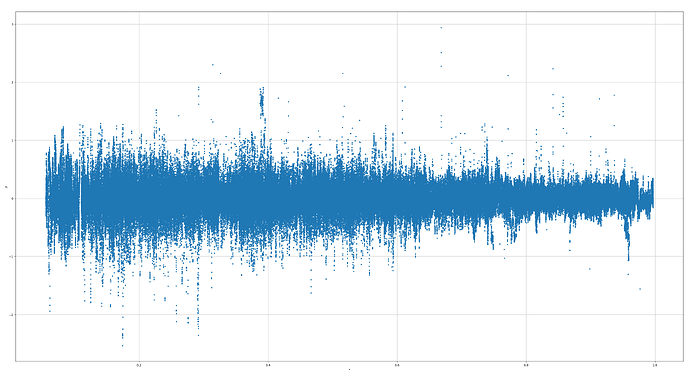
I am trying to estimate a conservative description of distribution p(y|x) (see image)
So far I am working with a MixtureDensityNetwork (estimating only 1 gaussian mixture and a negLogLikelihoodGaussian Loss) (Bishop94), resulting in a $\mu(x)$ and $\sigma^2(x)$.
But I would like to include a more conservative penalty term into the cost/loss function, as the underlying distribution is not necessarily a Gaussian one, such that in the end $\mu(x)$ and $\sigma^2(x)$ describe the data.
I came across the “Karush Kuhn Tuckert” conditions (for constraint optimization), so I wanted to ask you if any of you have already worked with it and incorporate it into the Loss function?
Best
Nerolf