Unexpected gradient of sum - doesn't match sum of gradients

autograd
1

Alright so this looks like such a simple issue that I’m afraid I’ve misunderstood some of the core workings of PyTorch/autograd.

My problem is straightforward: I have a gradient of a sum that turns out 0 while it shouldn’t be, and it doesn’t match the sum of the gradients separately.

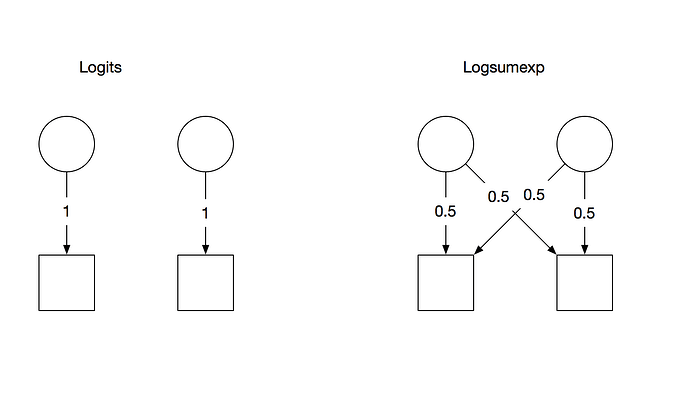
I’ve concocted a simplified example to illustrate. We’re in the probability domain, or rather, the logprob domain, so this is the straightforward approximation of probabilities using a softmax on top of a linear layer. Well, not quite a softmax, because logprobs. There are two output classes.

import torch
import torch.nn as nn
import torch.nn.functional as F

feat_dim, out_dim = 1, 2
encoder = nn.Linear(feat_dim, out_dim, bias=False)
nn.init.zeros_(encoder.weight.data)
# Fabricate some one-hot encoded data of batch size 1, good enough
batch_size = 1
input = torch.eye(feat_dim)[:batch_size]

As I said, I have the sum of gradients, or rather a difference really. Below I’ll show the gradients of the linear layer’s weights after backpropagating first the difference, then the summands themselves separately.

logits = encoder.forward(input)
norm = torch.logsumexp(logits, dim=1, keepdim=True)
(logits-norm).sum().backward()
print(encoder.weight.grad)
nn.init.zeros_(encoder.weight.grad.data)

logits = encoder.forward(input)
logits.sum().backward()
print(encoder.weight.grad)
nn.init.zeros_(encoder.weight.grad.data)

logits = encoder.forward(input)
norm = torch.logsumexp(logits, dim=1, keepdim=True)
norm.sum().backward()
print(encoder.weight.grad)

This gives (annotated):

# grad of logits - norm
tensor([[0.],
        [0.]])
# grad of logits
tensor([[1.],
        [1.]])
# grad of norm
tensor([[0.5000],
        [0.5000]])

The gradients for logits and norm are exactly what I expected. I expected the gradient for logprobs to be the difference of the gradients of logits and norm, but that’s not the case. Instead it’s zeros, for no conceivable reason.

I must be missing something incredibly simple. Maybe the gradient of norm gets backpropagated multiple times, but I don’t see it. Could anyone shed some light on the issue?

2

You can you look at your situation as finding derivative of f(g(h(w))), and the values you get are h’ = 1, g’=1/2 and f’=0 . Since this is composition, f’!=h’+g’

To see why specifically you get zero you can decorate your graph to print backward values

import torch
import torch.nn as nn
import torch.nn.functional as F

feat_dim, out_dim = 1, 2
encoder = nn.Linear(feat_dim, out_dim, bias=False)
nn.init.zeros_(encoder.weight.data)
batch_size = 1
input = torch.eye(feat_dim)[:batch_size]

def decorate(tensor, name):
    def print_backward(grad):
        print(f"({name}): ", grad)
    tensor.register_hook(print_backward)
    
logits = encoder.forward(input)
norm = torch.logsumexp(logits, dim=1, keepdim=True)
decorate(logits, 'logits')
decorate(logits, 'norm')
norm.expand_as(logits).backward(torch.ones_like(logits))

This prints following

(logits):  tensor([[1., 1.]])
(norm):  tensor([[1., 1.]])

Since both logits and norm vectors are 1’s, their difference will cancel out. The following is an illustration of how 1’s come about

41
411416×832 18.9 KB

1 Like
3

That is a beautifully crafted reply @Yaroslav_Bulatov. Many thanks for the informative graphic! And the illustration of how to use register_hook, that should come in useful in hte future.

It shows what really happens: PyTorch has summed up the partial derivatives over the different outputs. Which is why you’ve got 0.5 in the graphic, but only a 1D vector of derivatives in the backward hook.

I would still argue my original example of logits - norm is a sum however. And if I were to look at the partial derivatives individually, that sum would match. The problem was that I was looking at the sum of the derivatives (summed over outputs), which is what PyTorch gives us.

Anyway, cheers!