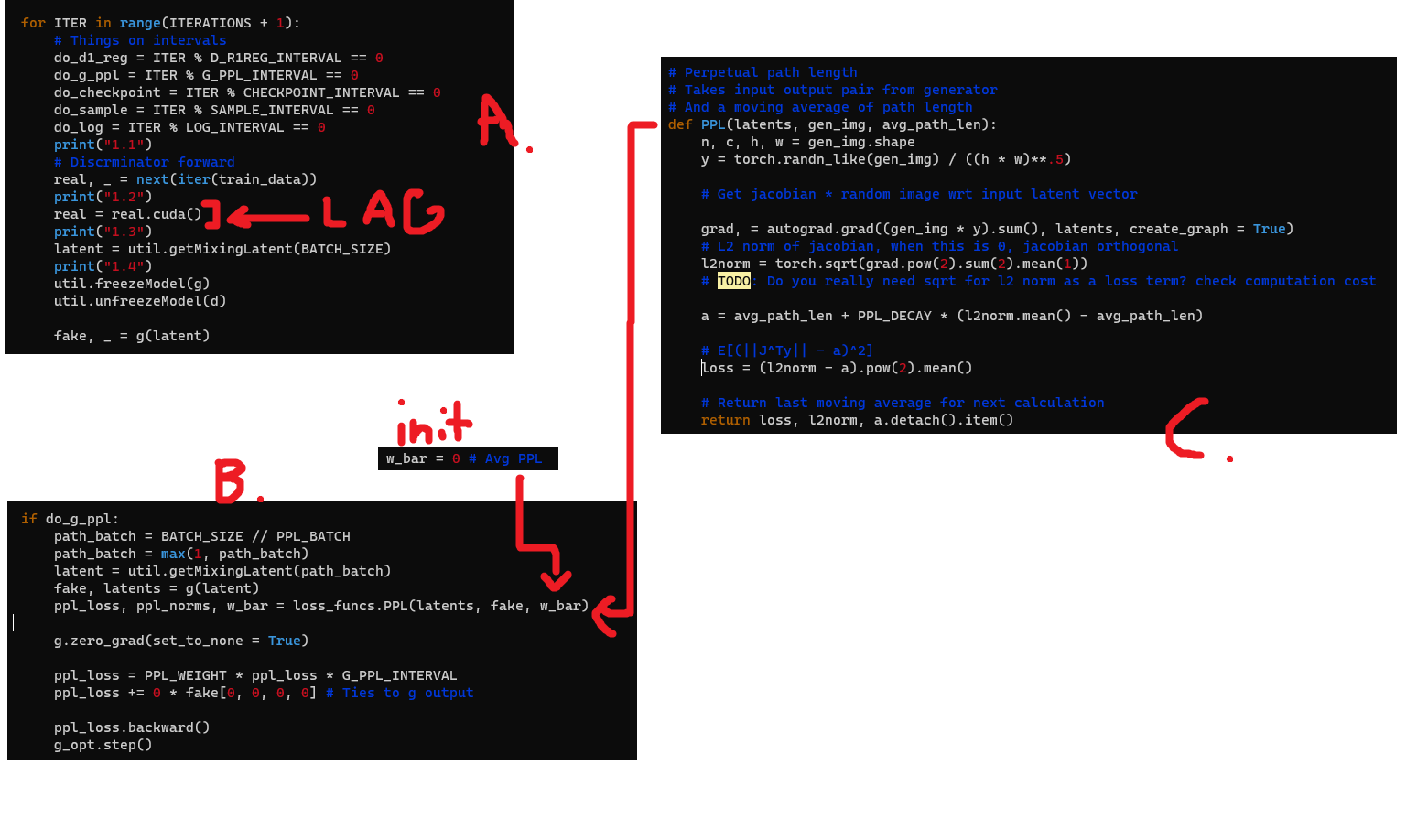
I’m using autograd for the first time (as in, I’ve never gone this low level before) and I think I’m doing it wrong. I would appreciate some help on finding what mistake I’m making. The issue is as follows:
A. runs every parameter update. B. runs every 4 parameter updates (in same loop as A) and calls C (where I use autograd.grad). On every iteration of the loop immediately following B being run, moving my training data to my GPU is really slow (as in, it takes multiple seconds). If I disable B entirely, this lag disappears and everything in A runs as fast as you’d expect. There is no noticeable lag during B or during any of the code that follows it, just at the point I’ve marked (moving my batch to gpu).
dataset = ImageFolder(data_path, transform = util.getImToTensorTF())
train_data = torch.utils.data.DataLoader(dataset, batch_size = BATCH_SIZE,
shuffle = True, pin_memory = True, num_workers = 0)
g_opt = torch.optim.AdamW(g.parameters(),
lr = LEARNING_RATE * G_PPL_INTERVAL / (G_PPL_INTERVAL + 1),
betas = (0, 0.99 ** (G_PPL_INTERVAL / (G_PPL_INTERVAL + 1))))
...
real, _ = next(iter(train_data))
real = real.cuda() # lag here (first cuda op in loop)
...
if do_g_ppl:
path_batch = BATCH_SIZE // PPL_BATCH
path_batch = max(1, path_batch)
latent = util.getMixingLatent(path_batch)
fake, latents = g(latent)
ppl_loss, ppl_norms, w_bar = loss_funcs.PPL(latents, fake, w_bar)
g.zero_grad(set_to_none = True)
ppl_loss = PPL_WEIGHT * ppl_loss * G_PPL_INTERVAL
ppl_loss += 0 * fake[0, 0, 0, 0] # Ties to g output
ppl_loss.backward()
g_opt.step()
Where the PPL loss is calculated by this function:
# Perpetual path length
# Takes input output pair from generator
# And a moving average of path length
def PPL(latents, gen_img, avg_path_len):
n, c, h, w = gen_img.shape
y = torch.randn_like(gen_img) / ((h * w)**.5)
# Get jacobian * random image wrt input latent vector
grad, = autograd.grad((gen_img * y).sum(), latents, create_graph = True)
# L2 norm of jacobian, when this is 0, jacobian orthogonal
l2norm = torch.sqrt(grad.pow(2).sum(2).mean(1))
# TODO: Do you really need sqrt for l2 norm as a loss term? check computation cost
a = avg_path_len + PPL_DECAY * (l2norm.mean() - avg_path_len)
# E[(||J^Ty|| - a)^2]
loss = (l2norm - a).pow(2).mean()
# Return last moving average for next calculation
return loss, l2norm, a.detach().item()