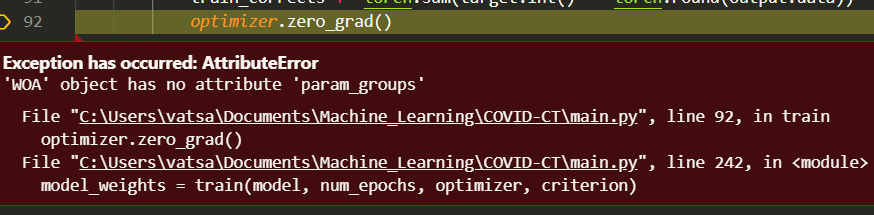
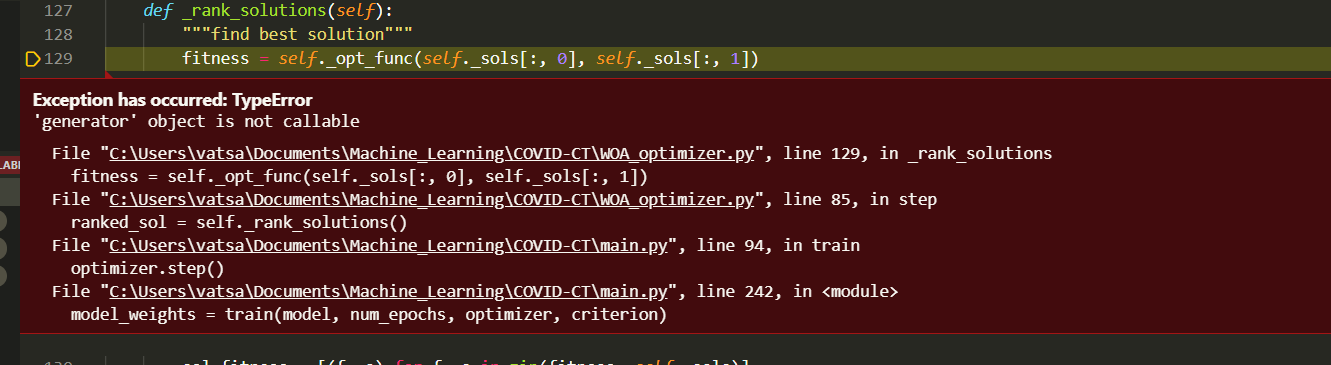
My study requires me to use a custom optimizer in my framework. I had written a script which used Adam optim from pytorch ecosystem. I want to WOA optimizer and I want to know what I need to do from zeroing the gradients so that I could easily implement using the prebuilt pipeline. I am getting trouble finding out what does specific optim.zero_grad() do since there’s no explicit mention of function in source code provided. I attaching the optimizer file too.
import torch
from torch.optim import Optimizer
import numpy as np
def schaffer(X, Y):
"""constraints=100, minimum f(0,0)=0"""
numer = np.square(np.sin(X**2 - Y**2)) - 0.5
denom = np.square(1.0 + (0.001*(X**2 + Y**2)))
return 0.5 + (numer*(1.0/denom))
def eggholder(X, Y):
"""constraints=512, minimum f(512, 414.2319)=-959.6407"""
y = Y+47.0
a = (-1.0)*(y)*np.sin(np.sqrt(np.absolute((X/2.0) + y)))
b = (-1.0)*X*np.sin(np.sqrt(np.absolute(X-y)))
return a+b
def booth(X, Y):
"""constraints=10, minimum f(1, 3)=0"""
return ((X)+(2.0*Y)-7.0)**2+((2.0*X)+(Y)-5.0)**2
def matyas(X, Y):
"""constraints=10, minimum f(0, 0)=0"""
return (0.26*(X**2+Y**2))-(0.48*X*Y)
def cross_in_tray(X, Y):
"""constraints=10,
minimum f(1.34941, -1.34941)=-2.06261
minimum f(1.34941, 1.34941)=-2.06261
minimum f(-1.34941, 1.34941)=-2.06261
minimum f(-1.34941, -1.34941)=-2.06261
"""
B = np.exp(np.absolute(100.0-(np.sqrt(X**2+Y**2)/np.pi)))
A = np.absolute(np.sin(X)*np.sin(Y)*B)+1
return -0.0001*(A**0.1)
def levi(X, Y):
"""constraints=10,
minimum f(1,1)=0.0
"""
A = np.sin(3.0*np.pi*X)**2
B = ((X-1)**2)*(1+np.sin(3.0*np.pi*Y)**2)
C = ((Y-1)**2)*(1+np.sin(2.0*np.pi*Y)**2)
funcs = {'schaffer':schaffer, 'eggholder':eggholder, 'booth':booth, 'matyas':matyas, 'cross':cross_in_tray, 'levi':levi}
func_constraints = {'schaffer':100.0, 'eggholder':512.0, 'booth':10.0, 'matyas':10.0, 'cross':10.0, 'levi':10.0}
func = 'booth'
nsols = 50
ngens = 30
C = func_constraints[func]
constraints = [[-C, C], [-C, C]]
opt_func = funcs[func]
b = 0.5
a = 2.0
a_step = a/ngens
maximize = False
class WOA(Optimizer):
def __init__(self, opt_func, constraints=constraints, nsols=nsols, b=b, a=a, a_step=a_step,maximize=maximize):
self._opt_func = opt_func
self._constraints = constraints
self._sols = self._init_solutions(nsols)
self._b = b
self._a = a
self._a_step = a_step
self._maximize = maximize
self._best_solutions = []
def get_solutions(self):
"""return solutions"""
return self._sols
def step(self):
"""solutions randomly encircle, search or attack"""
ranked_sol = self._rank_solutions()
best_sol = ranked_sol[0]
#include best solution in next generation solutions
new_sols = [best_sol]
for s in ranked_sol[1:]:
if (np.random.uniform(0.0, 1.0)) > 0.5:
A = self._compute_A()
norm_A = torch.linalg.norm(A)
if norm_A < 1.0:
new_s = self._encircle(s, best_sol, A)
else:
###select random sol
random_sol = self._sols[torch.randint(self._sols.shape[0])]
new_s = self._search(s, random_sol, A)
else:
new_s = self._attack(s, best_sol)
new_sols.append(self._constrain_solution(new_s))
self._sols = torch.stack(new_sols)
self._a -= self._a_step
def _init_solutions(self, nsols):
"""initialize solutions uniform randomly in space"""
sols = []
for c in self._constraints:
sols.append(torch.from_numpy(np.random.uniform(c[0], c[1], size=nsols)))
sols = torch.stack(sols, axis=-1)
return sols
def _constrain_solution(self, sol):
"""ensure solutions are valid wrt to constraints"""
constrain_s = []
for c, s in zip(self._constraints, sol):
if c[0] > s:
s = c[0]
elif c[1] < s:
s = c[1]
constrain_s.append(s)
return constrain_s
def _rank_solutions(self):
"""find best solution"""
fitness = self._opt_func(self._sols[:, 0], self._sols[:, 1])
sol_fitness = [(f, s) for f, s in zip(fitness, self._sols)]
#best solution is at the front of the list
ranked_sol = list(sorted(sol_fitness, key=lambda x:x[0], reverse=self._maximize))
self._best_solutions.append(ranked_sol[0])
return [ s[1] for s in ranked_sol]
def print_best_solutions(self):
print('generation best solution history')
print('([fitness], [solution])')
for s in self._best_solutions:
print(s)
print('\n')
print('best solution')
print('([fitness], [solution])')
print(sorted(self._best_solutions, key=lambda x:x[0], reverse=self._maximize)[0])
def _compute_A(self):
r = torch.from_numpy(np.random.uniform(0.0, 1.0, size=2))
return (2.0*torch.multiply(self._a, r))-self._a
def _compute_C(self):
return 2.0*torch.from_numpy(np.random.uniform(0.0, 1.0, size=2))
def _encircle(self, sol, best_sol, A):
D = self._encircle_D(sol, best_sol)
return best_sol - torch.multiply(A, D)
def _encircle_D(self, sol, best_sol):
C = self._compute_C()
D = torch.linalg.norm(torch.multiply(C, best_sol) - sol)
return D
def _search(self, sol, rand_sol, A):
D = self._search_D(sol, rand_sol)
return rand_sol - torch.multiply(A, D)
def _search_D(self, sol, rand_sol):
C = self._compute_C()
return torch.linalg.norm(torch.multiply(C, rand_sol) - sol)
def _attack(self, sol, best_sol):
D = torch.linalg.norm(best_sol - sol)
L = torch.from_numpy(np.random.uniform(-1.0, 1.0, size=2))
return torch.multiply(torch.multiply(D,torch.exp(self._b*L)), torch.cos(2.0*np.pi*L))+best_sol
Thanks for your help