Vectorized 6 loops or convert to Pytorch operations for efficient computation

1

Hi.
I would like to rewrite this code in a Pytorch-like and vectorized form for efficient computation.

import torch

num_faces = 10
max_m = 5
C2 = torch.rand(num_faces,max_m,max_m,max_m)
C3 = torch.rand(num_faces,max_m,max_m,max_m)


# This is the naive slow implementation with 6 loops, but is correct
D_abc_correct = torch.zeros(num_faces,max_m,max_m,max_m)
for a in range(max_m):
    for b in range(max_m):
        for c in range(max_m):
            for i2 in range(a+1):
                for j2 in range(b+1):
                    for k2 in range(c+1):
                        D_abc_correct[:,a,b,c] += C2[:,i2,j2,k2]*C3[:,a-i2,b-j2,c-k2]

A slightly optimized version with 3 loops, also correct

# 
D_abc = torch.zeros(num_faces,max_m,max_m,max_m)
for a in range(max_m):
    for b in range(max_m):
        for c in range(max_m):
            D_abc[:,a,b,c] = (C2[:,:(a+1),:(b+1),:(c+1)]*(C3[:,:(a+1),:(b+1),:(c+1)]).flip([1,2,3])).sum([1,2,3])

Any changes after that lead to some mismatch shape

# Check the results

print(torch.allclose(D_abc, D_abc_correct))
# True
print(D_abc.shape)
#torch.Size([10, 5, 5, 5])

Thanks

2

On StackOverflow python - Vectorized 6 loops or convert to Pytorch/numpy operations for efficient computation - Stack Overflow

3

It seems like a simplified minimal problem in 1D is as follows

max_m = 10

c2 = torch.rand(max_m)
c3 = torch.rand(max_m)
d =torch.zeros(max_m)

for a in range(max_m):
    d[a] = (c2[:(a+1)]*(c3[:a+1].flip([0]))).sum(0)

It seems like you want to perform an inner product over the two tensors, but with varying lengths.

I couldn’t solve it yet but am putting this here in case it is useful as a minimal example for others.

4

Hi Jean Paul!

Here’s the best I could come up with for a loop-free version:

At the cost of materializing a large, nine-dimensional “contraction-kernel”
tensor, you can replace the six for-loops with a single einsum() call.

Here is a script that implements this:

import torch
print (torch.__version__)

_ = torch.manual_seed (2023)

num_faces = 10
max_m = 5
C2 = torch.rand(num_faces,max_m,max_m,max_m)
C3 = torch.rand(num_faces,max_m,max_m,max_m)

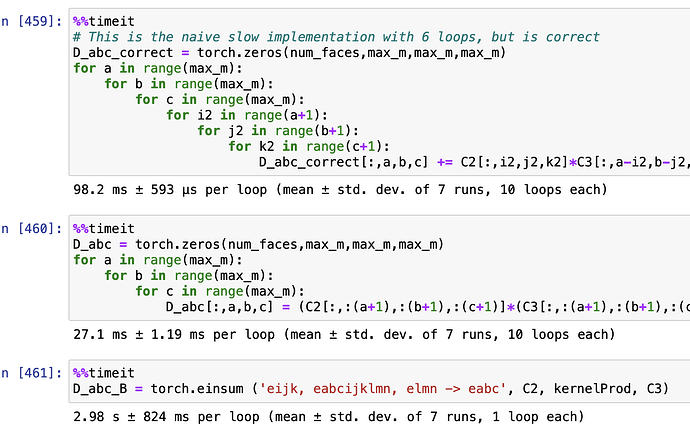
# This is the naive slow implementation with 6 loops, but is correct
D_abc_correct = torch.zeros(num_faces,max_m,max_m,max_m)
for a in range(max_m):
    for b in range(max_m):
        for c in range(max_m):
            for i2 in range(a+1):
                for j2 in range(b+1):
                    for k2 in range(c+1):
                        D_abc_correct[:,a,b,c] += C2[:,i2,j2,k2]*C3[:,a-i2,b-j2,c-k2]

# set up "contraction kernel"
inds = torch.arange (max_m)
kernel = ((inds.unsqueeze (0) + inds.unsqueeze (1)).unsqueeze (0) == inds.unsqueeze (-1).unsqueeze (-1)).float()

print ('check one slice of kernel:')
print (kernel[2])   # check one slice to see what it looks like

kernelProd = torch.einsum ('ail, bjm, ckn -> abcijklmn', kernel, kernel, kernel)   # "outer-product" kernel
print ('kernelProd is big, but rather sparse:')
print ('numel():     ', kernelProd.numel())                                        # quite big
print ('num-zero:    ', (kernelProd == 0.0).sum().item())                          # with lots of zeros
print ('frac-nonzero:', (kernelProd != 0.0).sum().item() / kernelProd.numel())     # so rather sparse
kernelProd = kernelProd.unsqueeze (0).expand (num_faces, -1, -1, -1, -1, -1, -1, -1, -1, -1)   # expand() view with num_faces dimension

D_abc_B = torch.einsum ('eijk, eabcijklmn, elmn -> eabc', C2, kernelProd, C3)

# check einsum result
print ('torch.allclose (D_abc_correct, D_abc_B):', torch.allclose (D_abc_correct, D_abc_B))

And here is its output:

2.0.0
check one slice of kernel:
tensor([[0., 0., 1., 0., 0.],
        [0., 1., 0., 0., 0.],
        [1., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.],
        [0., 0., 0., 0., 0.]])
kernelProd is big, but rather sparse:
numel():      1953125
num-zero:     1949750
frac-nonzero: 0.001728
torch.allclose (D_abc_correct, D_abc_B): True

Note, you can reuse kernelProd, so even if you have to run this
computation multiple times for differing values of the input tensors,
C2 and C3, you only have to construct kernelProd once.

Best.

K. Frank

1 Like
5

It seems like a further optimization can be performed using convolutions.

The issue is now vectorizing the operation over num_faces since performing convolutions over a set of pairs of tensors doesn’t seem to be supported.

Here is an implementation of the minimal problem in 1D:

import torch
import torchaudio
torch.__version__

max_m = 10

c2 = torch.rand(max_m)
c3 = torch.rand(max_m)
d_two =torch.zeros(max_m)
d_one =torch.zeros(max_m)

# Naive implementation with two loops
d_two = torch.zeros(max_m)
for a in range(max_m):
    for i in range(a+1):
        d_two[a] += c2[i]*c3[a-i]
        
# Better implementation with innermost loop vectorized
for a in range(max_m):
    d_one[a] = (c2[:(a+1)]*(c3[:a+1].flip([0]))).sum(0)
    
# No loops, with convolution operation
d_conv = torchaudio.functional.convolve(c2,c3,'full')[0:max_m]

print(torch.allclose(d_two,d_one))
print(torch.allclose(d_two,d_conv))
6

This is quite an elegant solution to the problem. Unfortunately it seems that it runs much slower than even the 6 loop implementation:

image
image1500×944 120 KB

Perhaps @jpainam might want to try running on their GPU to compare results?

7

I’m curious if there is some overhead associated with the first time torch.einsum is used and whether a warmup would be necessary. Does %%timeit do a warmup iteration?

8

@KFrank provided a great implementation. I am putting in order all the snippets, with my optimization at the end, which runs fastest.

import torch
print (torch.__version__)
_ = torch.manual_seed (2023)

num_faces = 1000
max_m = 5
C2 = torch.rand(num_faces,max_m,max_m,max_m)
C3 = torch.rand(num_faces,max_m,max_m,max_m)

# set up "contraction kernel"
inds = torch.arange (max_m)
kernel = ((inds.unsqueeze (0) + inds.unsqueeze (1)).unsqueeze (0) == inds.unsqueeze (-1).unsqueeze (-1)).float()
kernelProd = torch.einsum ('ail, bjm, ckn -> abcijklmn', kernel, kernel, kernel)
kernelProd = kernelProd.unsqueeze (0).expand (num_faces, -1, -1, -1, -1, -1, -1, -1, -1, -1)   # expand() view with num_faces dimension





D_abc_correct = torch.zeros(num_faces,max_m,max_m,max_m)
for a in range(max_m):
    for b in range(max_m):
        for c in range(max_m):
            for i2 in range(a+1):
                for j2 in range(b+1):
                    for k2 in range(c+1):
                        D_abc_correct[:,a,b,c] += C2[:,i2,j2,k2]*C3[:,a-i2,b-j2,c-k2]



D_abc = torch.zeros(num_faces,max_m,max_m,max_m)
for a in range(max_m):
    for b in range(max_m):
        for c in range(max_m):
            D_abc[:,a,b,c] = (C2[:,:(a+1),:(b+1),:(c+1)]*(C3[:,:(a+1),:(b+1),:(c+1)]).flip([1,2,3])).sum([1,2,3])




D_abc_B = torch.einsum ('eijk, eabcijklmn, elmn -> eabc', C2, kernelProd, C3)



D_abc_C = torch.einsum ('eijk, ail, bjm, ckn, elmn -> eabc', C2, kernel, kernel, kernel, C3)



print(torch.allclose (D_abc_correct, D_abc))
print(torch.allclose (D_abc_correct, D_abc_B))
print(torch.allclose (D_abc_correct, D_abc_C))

All the results are correct:

2.0.1
True
True
True

Timing the different versions:

image
image2182×1034 244 KB

9

It doesn’t seem to be the case. I put an optimized version of @KFrank 's code, which now runs faster than the three loop implementation.

I swapped the order when running '%%timeit ’ to run KFrank’s code and its optimized versions just to make sure, the results are the same

image
image2188×388 45.5 KB

image
image2218×378 45.2 KB

10

Hi Osama!

Yes, this is much better. Materializing kernelProd is wasteful and
unnecessary.

Best.

K. Frank

1 Like