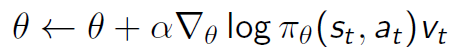Just in case it’s useful, I can reproduce the results from calling .reinforce with the following code:
"""
Try some reinforce by hand and similar
"""
import torch
from torch import autograd, nn, optim
import torch.nn.functional as F
from torch.autograd import Variable
import numpy as np
def run_model(x, h1):
torch.manual_seed(123)
params = list(h1.parameters())
x1 = h1(Variable(x))
x2 = F.softmax(x1)
a = torch.multinomial(x2)
print('a', a)
return x1, x2, a
def run_by_hand(params, x, h1):
print('')
print('=======')
print('by hand')
h1.zero_grad()
x1, x2, a = run_model(x, h1)
g = torch.gather(x2, 1, Variable(a.data))
log_g = g.log()
log_g.backward(- torch.ones(4, 1))
print('params.grad', params.grad)
def run_pytorch_reinforce(params, x, h1):
print('')
print('=======')
print('pytorch reinforce')
h1.zero_grad()
x1, x2, a = run_model(x, h1)
a.reinforce(torch.ones(4, 1))
autograd.backward([a], [None])
print('params.grad', params.grad)
def run():
N = 4
K = 1
C = 3
torch.manual_seed(123)
x = torch.ones(N, K)
h1 = nn.Linear(K, C, bias=False)
params = list(h1.parameters())[0]
run_by_hand(params, x, h1)
run_pytorch_reinforce(params, x, h1)
if __name__ == '__main__':
run()
Result:
=======
by hand
a Variable containing:
1
1
0
1
[torch.LongTensor of size 4x1]
params.grad Variable containing:
0.6170
-1.3288
0.7117
[torch.FloatTensor of size 3x1]
=======
pytorch reinforce
a Variable containing:
1
1
0
1
[torch.LongTensor of size 4x1]
params.grad Variable containing:
0.6170
-1.3288
0.7117
[torch.FloatTensor of size 3x1]
(Its actually almost the same amount of code in fact?)