Dunno if autograd is the right category for this question. There’s a related thread here but I didn’t see an official answer.
My current guess is that torch use this paper for it [1806.01851] Pathwise Derivatives Beyond the Reparameterization Trick, which is different from what tensorflow-probability uses, which is the implicit reparam gradient from DeepMind. I looked through the code base but couldn’t find a concrete reference unlike the tensorflow-probability code that explicitly mentions they use the implicit reparam gradient.
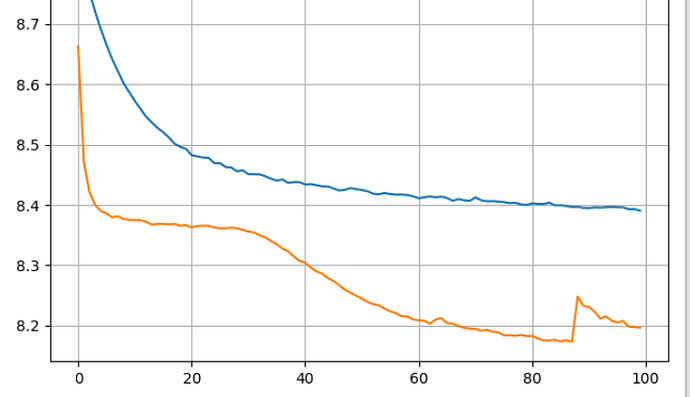
The reason that I am asking is because I am trying to do stochastic gradient based training of LDA, the tensorflow-probability version trains nicely, but my pytorch implementation’s gradient tend to blow up, and need special handling. 1 example of such training instability can be seen below, where there’s a significant kink near the end of training for the orange curve, and this happens consistently. This time it recovered but it can blow up at other times.
The tfp code and the pytorch code I wrote are identical down to the initialization scheme, and the tfp code’s optimization curve follows almost exactly like the orange curve, but without the kinks.
Mentioning @fritzo @neerajprad you guys because based on my search on github you guys contribute to the pyro/torch.distributions a lot.
If we are not using the implicit reparametrization, I will probably request one on github.