There are nn.Softmax, torch.nn.functional.softmax and torch.nn.functional.log_softmax, but what is your best recommendation? And what’s the difference between them?
nn.Softmax vs nn.functional.softmax
If you take a look at the source code for nn.Softmax, then you can see that in the forward method it actually calls nn.functiona.softmax (functional is imported as F then it is written as F.softmax).
So it is the same and if you want to do some functional stuff, then you can use this way.
However, if you want it to be an actual layer and not just a functional method, then I would recommend defining a layer with the constructor. If you use functional instead of a layer at the forward method of your architecture, then if someone tries to extract the children and put them in a container (e.g. nn.Sequential), the functional stuff will not be done. If this is not clear then I can give you an example.
Softmax vs LogSoftmax
As you can see, both activation functions are the same, only with a log.
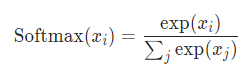
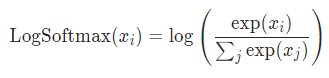
As you might already know, the result of softmax are probabilities between 0 and 1. This is something useful for us to understand.
Log
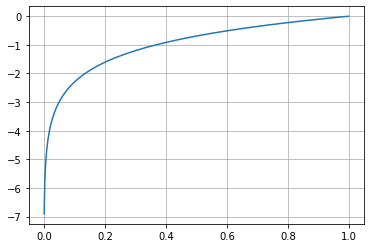
If you plot the values between 0 and 1 for log, you get the following plot. Here, values closer to 0 are heavily penalized.
Example
We can look at a little example.
soft = torch.nn.Softmax(dim=0)
log_soft = torch.nn.LogSoftmax(dim=0)
x = torch.rand(3)
print(x)
#tensor([0.6848, 0.1505, 0.5071])
If we print the softmax values, we can understand that the first value is about 40% sure to be the correct class. The third class is very close but still a little bit smaller. The second class is much lower, thus less likely to be the correct one.
print(soft(x))
#tensor([0.4127, 0.2418, 0.3455])
If we now print the logsoft values, we can sort of understand from the graph above that values closer to 0 are more likely to be the correct class. But other than, it will be difficult for us to determine how good the estimate is.
print(log_soft(x))
#tensor([-0.8851, -1.4195, -1.0628])
Which one should you use
Here is more information on as to why the log version might behave better for improved numerical performance and gradient optimization.
Here is another answer on the topic.
But I would suggest trying different approaches and see which works better for your problem. There is not going to be a single function that will be the optimal solution for every problem.
I personally like using CrossEntropyLoss, which makes use of LogSoftmax. But I think the best thing is to try and see what works best.
Hope this helps ![]()