hyuntae
(Hyuntae Choi)
1
Hi.
I have a short question about “torch.nn.L1Loss()”.
As we know, it is not possible to differentiate |x| when x is zero (because the derivative of |x| is x/|x|).
However, when I used torch.nn.L1Loss() with network, loss.backward() worked…
How is it possible?
Also, would you explain how it is possible to calculate gradient of L1 Loss in pytorch when x is zero?
Thanks.
1 Like
spanev
(Serge Panev)
2
What is x in your example? Is it the input of the model?
Let’s say x your input (with requires_grad=True) and the first layer of the model in a Linear with no bias, parameters w, doing y = w*x.
The last step of the backprop would be dL/dx = dy/dx * dL/dy
and dy/dx = w, no matter what is the value of x.
hyuntae
(Hyuntae Choi)
3
Thanks for reply. And sorry for confusing.
x is just a variable of the equation ‘y = |x|’, not the input or output of network.
I just wonder when try to differentiate the y = |x|, how the torch handle when x is 0 although it is impossible to differentiate at that point.
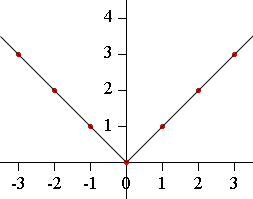
spanev
(Serge Panev)
4
Ok, my bad, I mistook the pipes in |x| for l.
I think it uses an approximate gradient on 0. And as you can see here, it considers 0 as a positive input.
1 Like
hyuntae
(Hyuntae Choi)
5
Thank you very much!
Then, I need to find the implementation of approximate.
Thanks!
