Where is the source code for MulBackward1

autograd
1

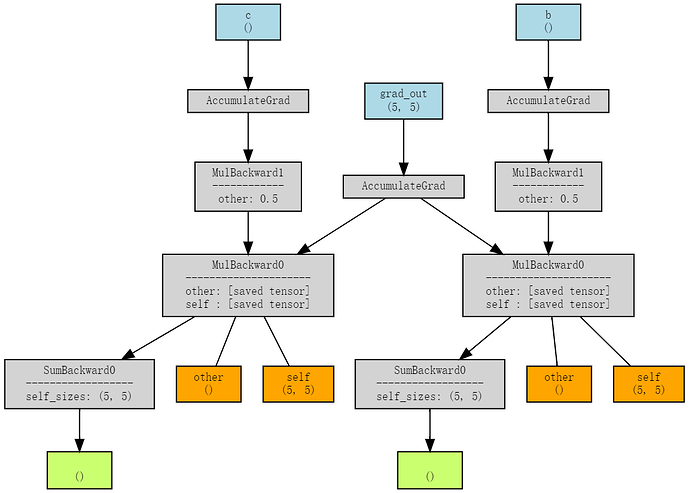
I’m using pytorch 1.8.1. As I’m running a testcase in test_autograd.py, e.g. addcmul. I see there is a gradgradcheck to check the second order derivatives. I just want to know how the backward is done.
So I used torchviz to generate the backward graph below:

addcmul
addcmul1106×791 44.6 KB
(This graph is generated in an pytorch 1.9 environment)
So, I guess these are the called backward functions, right? I want to know how MulBackward1 is done in pytorch c/cuda source code. But I greped and only found it here:build/lib.linux-x86_64-3.6/torch/include/torch/csrc/autograd/generated/Functions.h.(And from the directory hierachy, it seems this file is auto generated, maybe from some macros?) So it’s superclass is TraceableFunction and the superclass of that is Node. But I cann’t find anything like how MulBackward1 is implemented, like an op. Or am I looking into the wrong direction?

2

By using nvprof, I managed to trace it down to this kernel information:

void at::native::unrolled_elementwise_kernel<at::native::MulScalarFunctor<double, double>, at::detail::Array<char*, 2>, Trivi...(int, at::native::MulScalarFunctor<double, double>, at::detail::Array<char*, 2>, TrivialOffsetCalculator<1, unsigned int>, TrivialOffsetCalculator<1, unsigned int>, at::native::memory::LoadWithCast<1>, at::native::memory::StoreWithCast)

And another kernel is

void at::native::unrolled_elementwise_kernel<at::native::MulFunctor<float>, at::detail::Array<char*, 3>, OffsetCalculator<2, ...(int, at::native::MulFunctor<float>, at::detail::Array<char*, 3>, OffsetCalculator<2, unsigned int>, OffsetCalculator<1, unsigned int>, at::native::memory::LoadWithoutCast, at::native::memory::StoreWithoutCast)

I guess MulFunctor is for same shape multiplication? (MulBackward),
MulScalarFunctor is for an array times a scalar? (MulBackward1).
But I’m also quite curious as how did pytorch auto-generated MulBackward and MulBackward1, etc as in torch/csrc/autograd/generated/Functions.h file.

Edit:
for adcmul op, the torchviz result:
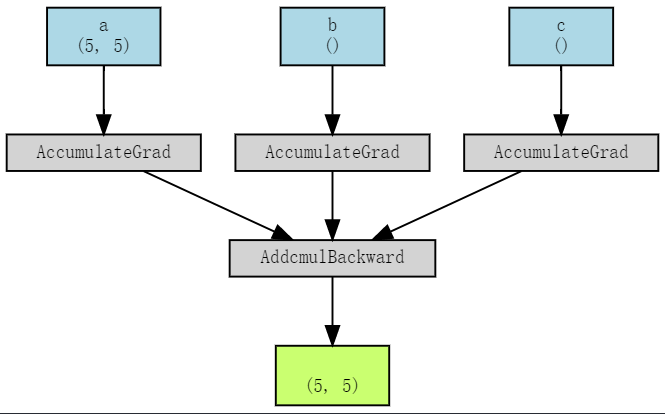
image
There is a AddcmulBackward, by inspecting into the kernels called using nvprof again, I also see that there is the aforemetioned at::native::MulScalarFunctor like for MulBackward1, but this time the template class is float:

void at::native::vectorized_elementwise_kernel<4, at::native::MulScalarFunctor<float, float>, at::detail::Array<char*, 2> >(int, at::native::MulScalarFunctor<float, float>, at::detail::Array<char*, 2>)

So, I’m curious why in the first case, it’s a double, in the second case, it’s a float?

And here is the simple python test code:

import torch

from torch import nn

from torchviz import make_dot, make_dot_from_trace

# %%

S = 2

device = 'cuda:0'

a = torch.randn(S, S, requires_grad=True, device=device)

b = torch.tensor(0.3, requires_grad=True, device=device)

c = torch.tensor(0.5, requires_grad=True, device=device)

value = 0.5

y = torch.addcmul(a, b, c, value=value)

# %%

# Use a fn to do addcmul/addcdiv, etc

def fn(*inputs):

    output = getattr(inputs[0], 'addcmul')(*inputs[1:], value=value)

    return output

num_outputs = 1

tupled_inputs = (a, b, c)

output = fn(*tupled_inputs)

# torch.allclose(output, a.addcmul(b, c, value=value))

# %%

grad_out = torch.ones_like(output, requires_grad=True)

def new_func(*args):

    input_args = args[:-num_outputs]

    grad_outputs = args[-num_outputs:]

    outputs = fn(*input_args)

    input_args = tuple(x for x in input_args if isinstance(x, torch.Tensor) and x.requires_grad)

    grad_inputs = torch.autograd.grad(outputs, input_args, grad_outputs, create_graph=True)

    return grad_inputs

tupled_inputs = (a, b, c, grad_out)

# %%

grad_inputs = new_func(*tupled_inputs)

# print(grad_inputs)

# Now try gradgrad

g_b = grad_inputs[1]

gradgrad_out = torch.ones_like(g_b, memory_format=torch.legacy_contiguous_format)

gradgrad_input = torch.autograd.grad(g_b, tupled_inputs, gradgrad_out,

                                              retain_graph=True, allow_unused=True)

# print(gradgrad_input[2])                                           

# # %%

# make_dot(output)

# # %%

# grad_inputs = new_func(*tupled_inputs)

# # %%

# grad_inputs[0]

# # %%

# make_dot(new_func(*tupled_inputs)[1], params={'a': a, 'b': b, 'c': c, 'grad_out': tupled_inputs[-1]})

# # %%

# make_dot(new_func(*tupled_inputs)[2], params={'a': a, 'b': b, 'c': c, 'grad_out': tupled_inputs[-1]})

# # %%

# make_dot(new_func(*tupled_inputs), params={'a': a, 'b': b, 'c': c, 'grad_out': tupled_inputs[-1]})

# # %%

# make_dot(new_func(*tupled_inputs), params={'a': a, 'b': b, 'c': c, 'grad_out': tupled_inputs[-1]}, show_attrs=True)

# # %%

# torch.__version__

With nvprof:

nvprof --print-gpu-trace python test_addcmul.py
3

It’s generated during the build in torch/csrc/autograd/generated. In Functions.cpp:

variable_list MulBackward1::apply(variable_list&& grads) {
  IndexRangeGenerator gen;
  auto self_ix = gen.range(1);
  variable_list grad_inputs(gen.size());
  auto& grad = grads[0];
  bool any_grad_defined = any_variable_defined(grads);
  if (should_compute_output({ self_ix })) {
    auto grad_result = any_grad_defined ? (mul_tensor_backward(grad, at::scalar\
_to_tensor(other), self_scalar_type)) : Tensor();
    copy_range(grad_inputs, self_ix, grad_result);
  }
  return grad_inputs;
}

and some not so interesting Python wrapping in python_functions.cpp

The above is generated by the things in tools/autograd processing derivatives.yaml.

4

Thank you very much. But I just checked my build files, I only see header files under torch/csrc/autograd/generated:

  • Functions.h
  • python_functions.h
  • variable_factories.h
  • VariableType.h

Is there environment variables which might controll if cpp files will be generated or not?

5

I never know, but it would seem that PyTorch should generate a number of .cpps as well:

6

Thanks a lot. I was using VSCode to search for this “Functions.cpp” file, the reason why I can’t find it is due to the directory is makred in .gitignore file. Now I commented it out from .gitignore file, I can find all the generated files. Again, thanks.
Besides, by reading the source code, for my case, I just figured out why the second case the templated parameters are all double, but not the first.

  1. For the first MulScalar<float, float> call, this happens during addcmul’s backward function. By checking the backward formula in “derivatives.yaml” file for addcmul:
- name: addcmul(Tensor self, Tensor tensor1, Tensor tensor2, *, Scalar value=1) -> Tensor

  self: handle_r_to_c(self.scalar_type(), grad)

  tensor1: handle_r_to_c(tensor1.scalar_type(), grad * (tensor2 * value).conj())

  tensor2: handle_r_to_c(tensor2.scalar_type(), grad * (tensor1 * value).conj())

It didn’t call another implemented backward function, instead, it writes down the calculation formula using already known operators, here it is mul, specifically, for tensor2 * value, it would be a tensor * Scalar, so it will call aten/src/ATen/native/BinaryOps.cpp mul():

Tensor mul(const Tensor& self, Scalar other) {
  return native::mul(self, wrapped_scalar_tensor(other));
}

Notice that it will call a wrapped_scalar_tensor() API to the Scalar variable first, by checking the source code for this, it will in fact call a set_wrapped_numer() function, which means when calculating the common_types for self(float) and other(double), the other’s type won’t participate in the calculation, so the result is float.
However, if we don’t use wrapped_scalar_tensor() API, the result of common_type would be double. That is the case of what happened when we do a backward for Mul for Scalar. Here in derivatives.yaml, you can find the following:

- name: mul.Scalar(Tensor self, Scalar other) -> Tensor
  self: mul_tensor_backward(grad, at::scalar_to_tensor(other), self.scalar_type())

Notice that in this backward function, it just directly called at::scalar_to_tensor(other), without calling tensor.unsafeGetTensorImpl()->set_wrapped_number(true);. Thus, the common_type of double and float would be double now. But on my platform, I can’t use double on GPU, that’s why it fails for me.

1 Like
7

Glad you solved it and thank you for sharing your insights.

Best regards

Thomas