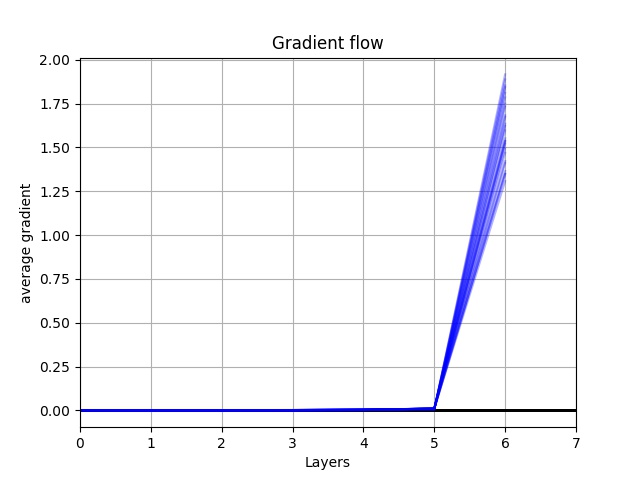
Hi There,
I add the second loss to my first loss and apply backward.(), but the gradient results after backward.() is as same as when I used just one loss. The first loss is nn.BCELoss() and the second loss is L1. I try different second loss , but does not have effect. It seems that backward.() does not create any gradient on the second loss regardless of type. I check the gradient flow just for the second loss which was 0. I am wondering if you have any ideas.
optimizerG = optim.Adam(netG.parameters(), lr=lr2, betas=(beta1, 0.999))
netG = Generator994(ngpu,nz,ngf).to(device)
## -----------------------------------------------------
for p in netG.parameters():
p.requires_grad = True
netG.zero_grad()
label.fill_(real_label)
label=label.to(device)
output = netD(fake).view(-1)
# Calculate G's loss based on this output
loss1 = criterion(output, label)
hist_rGau= np.histogram(Gaussy.squeeze(1).view(-1).detach().numpy(), bins=FFBins,range=[0 ,1])
count_r11 = hist_rGau[0]
PGAUSSY=count_r11/(count_r11.sum())
hist_rGAN = np.histogram(fake.squeeze(1).view(-1).detach().numpy(), bins=FFBins,range=[0 ,1])
count_r22 = hist_rGAN[0]
PGAN=count_r22/(count_r22.sum())
## -------- L1 loss and second loss---------------------------
loss2=abs(PGAUSSY-PGAN).sum()
## ----- total loss --------------------------
loss= loss1+loss2
loss=torch.tensor(loss,requires_grad=True)
loss=Variable(loss, requires_grad = True)
loss.backward()
for param in netG.parameters():
print(param.grad.data.sum())
optimizerG.step()
## --------------------------------------------------------
class Generator994(nn.Module):
def __init__(self,ngpu,nz,ngf):
super(Generator994, self).__init__()
self.ngpu=ngpu
self.nz=nz
self.ngf=ngf
self.l1= nn.Sequential(
# input is Z, going into a convolution
nn.ConvTranspose2d(self.nz, self.ngf * 8, 3, 1, 0, bias=False),
nn.BatchNorm2d(self.ngf * 8),
nn.ReLU(True),)
self.l2=nn.Sequential(nn.ConvTranspose2d(self.ngf * 8, self.ngf * 4, 3, 1, 0, bias=False),
nn.BatchNorm2d(self.ngf * 4),
nn.ReLU(True),)
self.l3=nn.Sequential(nn.ConvTranspose2d( self.ngf * 4, self.ngf * 2, 3, 1, 0, bias=False),
nn.BatchNorm2d(self.ngf * 2),
nn.ReLU(True),)
self.l4=nn.Sequential(nn.ConvTranspose2d( self.ngf*2, 1, 3, 1, 0, bias=False),nn.Sigmoid()
)
def forward(self, input):
out=self.l1(input)
out=self.l2(out)
out=self.l3(out)
out=self.l4(out)
return out