Why cant I see .grad of an intermediate variable?

21

Interesting stuff! I have 3 questions in connection (my first ever post here, so I beg for forgiveness about my greenness and the lengthy post :slight_smile:

I’m trying to implement GradNorm, a strategy to dynamically adapt weights for the individual loss contributions in a multi-task learning scenario. So, similar to your example and to the post of @hubert0527 think:

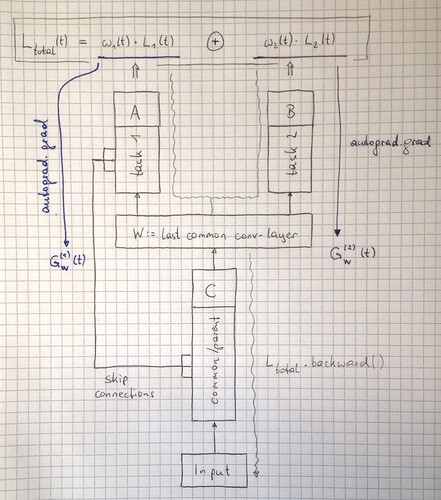
parent module C,

“ending” in some last common conv-layer having weights/bias {W}, feeding into individual

branch modules A and B,

such that for each training iteration (t)

Loss_total(t) = w1(t) * L1(t) + w2(t) * L2(t)

where w1(t) and w2(t) are the dynamically adjusted weights of each single-task loss.

C is a CNN with skip connections (concatenation of feature maps) to module A, which is another CNN, module B is a simple classifier with 3 fully connected layers. I’ll attach a sketch further down.

What one needs to calculate primarily is the norm of the gradient of each of the individual single-task losses w1 * L1 and w2 * L2 with respect to the network parameters {W} of the last common layer (the {W} are leaf variables), which can be done by:

GW_1 = || torch.autograd.grad(w1*L1, W) || (Eq 1 / task 1 / branch A)
GW_2 = || torch.autograd.grad(w2*L2, W) || (Eq 2 / task 2 / branch B)

Those are then further processed to update w1(t+1) and w2(t+1), and then the “normal” backward pass all the way back through module C needs to be performed.
Note that calling Loss_total.backward() does NOT yield GW_1 and GW_2 separately, but only their sum.

Here are my questions:

  1. If I execute (Eq 1) WITHOUT setting retain_graph=True, executing (Eq 2) gives the commonly known error for trying to backprop through one and the same (sub)graph twice, EVEN THOUGH the only thing those 2 subgraphs have in common is the parameters {W} at which they “end” so to speak. Why is that?

  2. The whole thing works if I set retain_graph=True in both the (Eq 1) and (Eq 2) executions and then execute Loss_total.backward(), but using the two retain_graph flags in the .grad-calls uses extra memory, which is kind of a waste.
    Why does the memory usage not peak at the end of the forward pass of the network, aren’t all the buffers needed in the .grad or .backward call(s) allocated exactly then?

  3. Is there any way of doing this without using any retain_graph=True (to save memory) and without doing several forward passes to regenerate the graph (to save time)?
    Maybe similar to the test example of @blackyang and @SimonW or also the test example of @smth in this post in several stages with a dummy variable, only that in my case it’s a bit different since I need the gradients of zz1 and zz2 w.r.t. the WEIGHTS of the final common layer, which would be the ‘3’ in yy = 3*xx of the test example, NOT w.r.t. the output yy of the final common layer. How could that be done?

Sketch:

image_1
image_11806×2046 791 KB

Long slide! Thanks to anyone who read this far. :wink:

4 Likes
22

Just in case anyone is still facing this problem, I usually use this code snippet to debug gradients:

def get_printer(msg):
    """This function returns a printer function, that prints information about a  tensor's
    gradient. Used by register_hook in the backward pass.
    """
    def printer(tensor):
        if tensor.nelement() == 1:
            print(f"{msg} {tensor}")
        else:
            print(f"{msg} shape: {tensor.shape}"
                  f" max: {tensor.max()} min: {tensor.min()}"
                  f" mean: {tensor.mean()}")
    return printer


def register_hook(tensor, msg):
    """Utility function to call retain_grad and Pytorch's register_hook
    in a single line
    """
    tensor.retain_grad()
    tensor.register_hook(get_printer(msg))

You just need to call register_hook and pass the tensor you want to see the gradients and a message that may help you to identify who is responsible for that gradient. I usually use it in conjunction with pdb.

4 Likes
23

Got any solution for this?

24

Awesome !!. This worked for me. Thanks @apaszke

25

Dear @bpetruzzo, I find myself in a very similar situation. Did you find any reason for this memory leak?

1 Like
26

divide yy into yy1 and yy2?