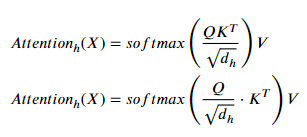Why denominator in multi-head attention in PyTorch's implementation different from most proposed structure?

annisat · March 31, 2022, 3:13pm

As the title describes. I just compared the code of transformers from hugging face’s Bert and torch.nn.Transformer, directly from the code I found in my site-packages. Specifically, I’m looking for the part of dividing attention score before softmax. Most paper on transformer mentioned this:

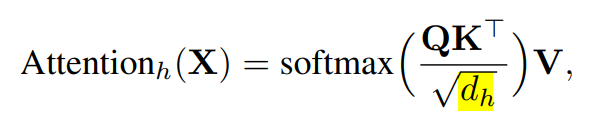
In hugging face’s Bert, I believe it is this line of code, which implement this quite right.

github.com

huggingface/transformers/blob/e4b234834a79541f31be227aadce13f5aafda85a/src/transformers/models/bert/modeling_bert.py#L324


      
              positional_embedding = positional_embedding.to(dtype=query_layer.dtype)  # fp16 compatibility
          
              if self.position_embedding_type == "relative_key":
                  relative_position_scores = torch.einsum("bhld,lrd->bhlr", query_layer, positional_embedding)
                  attention_scores = attention_scores + relative_position_scores
              elif self.position_embedding_type == "relative_key_query":
                  relative_position_scores_query = torch.einsum("bhld,lrd->bhlr", query_layer, positional_embedding)
                  relative_position_scores_key = torch.einsum("bhrd,lrd->bhlr", key_layer, positional_embedding)
                  attention_scores = attention_scores + relative_position_scores_query + relative_position_scores_key
          
          attention_scores = attention_scores / math.sqrt(self.attention_head_size)
          if attention_mask is not None:
              # Apply the attention mask is (precomputed for all layers in BertModel forward() function)
              attention_scores = attention_scores + attention_mask
          
          # Normalize the attention scores to probabilities.
          attention_probs = nn.functional.softmax(attention_scores, dim=-1)
          
          # This is actually dropping out entire tokens to attend to, which might
          # seem a bit unusual, but is taken from the original Transformer paper.
          attention_probs = self.dropout(attention_probs)

I believe the closest thing in PyTorch is this line, which is actually dividing query, not the result of dot product.

github.com

pytorch/pytorch/blob/6b0b088c6caef54d35ad04defe07a4a94831dd27/torch/nn/functional.py#L4999


      
                  and E is embedding dimension.
              - value: :math:`(B, Ns, E)` where B is batch size, Ns is the source sequence length,
                  and E is embedding dimension.
              - attn_mask: either a 3D tensor of shape :math:`(B, Nt, Ns)` or a 2D tensor of
                  shape :math:`(Nt, Ns)`.
          
              - Output: attention values have shape :math:`(B, Nt, E)`; attention weights
                  have shape :math:`(B, Nt, Ns)`
          """
          B, Nt, E = q.shape
          q = q / math.sqrt(E)
          # (B, Nt, E) x (B, E, Ns) -> (B, Nt, Ns)
          attn = torch.bmm(q, k.transpose(-2, -1))
          if attn_mask is not None:
              attn += attn_mask
          attn = softmax(attn, dim=-1)
          if dropout_p > 0.0:
              attn = dropout(attn, p=dropout_p)
          # (B, Nt, Ns) x (B, Ns, E) -> (B, Nt, E)
          output = torch.bmm(attn, v)
          return output, attn

I’d like to know if they’re really equivalent? Wouldn’t that change the amount of backpropagation into Wq and Qk?
I know training transformer from scratch is hard. I’m having trouble training torch.nn.Transformer from scratch in a recent project. But could this be a reason why the loss won’t go down?

Matias_Vasquez · March 31, 2022, 4:02pm

Since 𝑑_ℎ represents a scalar, it should not matter if you do it before or after the matrix multiplication.

Of course due to resolution you will get slightly different results, but I do not think that this should be enough reason for your loss to not go down. Here is a small example to show that there are differences, but they are very small.

import torch
import math

q = torch.rand(1, 5, 30)
k = torch.rand(1, 5, 30)
v = torch.rand(1, 5, 30)


B, Nt, E = q.shape
q_ = q / math.sqrt(E)
attn1 = torch.bmm(q_, k.transpose(-2, -1))
attn2 = torch.bmm(q, k.transpose(-2, -1)) / math.sqrt(E)

print(f"Attn1: {attn1}")
print(f"Attn2: {attn2}")
print(f"Compa: {attn1==attn2}")

# Output:
Attn1: tensor([[[1.4470, 1.2312, 1.4192, 1.0483, 1.0938],
         [1.5067, 1.2858, 1.3447, 1.3185, 1.2335],
         [1.3196, 1.1793, 1.3776, 1.1048, 1.0500],
         [1.2411, 1.1090, 1.3351, 0.9647, 0.9519],
         [1.6056, 1.5329, 1.6754, 1.3193, 1.4312]]])
Attn2: tensor([[[1.4470, 1.2312, 1.4192, 1.0483, 1.0938],
         [1.5067, 1.2858, 1.3447, 1.3185, 1.2335],
         [1.3196, 1.1793, 1.3776, 1.1048, 1.0500],
         [1.2411, 1.1090, 1.3351, 0.9647, 0.9519],
         [1.6056, 1.5329, 1.6754, 1.3193, 1.4312]]])
Compa: tensor([[[ True, False, False, False,  True],
         [False,  True,  True,  True, False],
         [ True, False, False, False,  True],
         [False,  True,  True, False, False],
         [False, False, False,  True, False]]])

Transformers do need a lot of training data and a lot of time to train. Would it be possible for you to take a pretrained model and fine tune it to your specific task?