I am trying to understand pytorch through a toy example of trying to train a perceptron to classify some data points. I am using a sigmoid for activation and binary cross entropy as my loss.
This is my code:
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import Dataset, DataLoader
import torch.optim as optim
import matplotlib.pyplot as plt
import numpy as np
# set random seed
torch.manual_seed(0)
# define perceptron
class Perceptron(nn.Module):
def __init__(self):
super(Perceptron,self).__init__()
self.linear = nn.Linear(in_features=2,out_features=1)
def forward(self,x):
x = self.linear(x)
x = torch.sigmoid(x)
return x
# create test data points
class testData(Dataset):
def __init__(self):
super(testData,self).__init__()
test_data = [([3,2],1),([1,1],0)]
self.data = test_data
def __getitem__(self,index):
dp,label = self.data[index]
dp = torch.FloatTensor(dp)
label = torch.tensor(label)
return dp,label
def __len__(self):
return len(self.data)
def main():
# epochs at which we plot the model
epoch_samples = [10,20,30,40,50,60,70,80,90,100]
fig,(ax1,ax2) = plt.subplots(nrows=2)
# plot the data points
ax1.scatter([3],[2],color='b')
ax1.scatter([1],[1],color='g')
# instantiate the model, optimiser and dataloader
model = Perceptron()
dataset = testData()
dataloader = DataLoader(dataset,batch_size=2)
optimiser = optim.SGD(model.parameters(),lr=1,weight_decay=0)
# train for 100 epochs
for epoch in range(101):
total_loss=0
for idx,batch in enumerate(dataloader):
dp,label = batch
preds = model(dp)
loss = F.binary_cross_entropy(preds.float(),label.unsqueeze(1).float())
optimiser.zero_grad()
loss.backward()
optimiser.step()
total_loss += loss.item()
# add model to plot if epoch in epoch samples list
if epoch in epoch_samples:
weights= model.linear.weight.detach().numpy()
w0 = weights[0,0]
w1 = weights[0,1]
bias = model.linear.bias.detach().numpy()[0]
x = np.linspace(0,5,50)
y = -((w0*x+bias)/w1)
# set the alpha coeffecient based on position of epoch in list
a = ((epoch_samples.index(epoch)+1)/len(epoch_samples))
# plot model
ax1.plot(x,y,color='r',alpha=a)
# add the abs weight value against epoch data point
ax2.scatter(epoch,[np.abs(w0)+np.abs(w1)],color='b')
# output the plot
plt.show()
if __name__ == "__main__":
main()
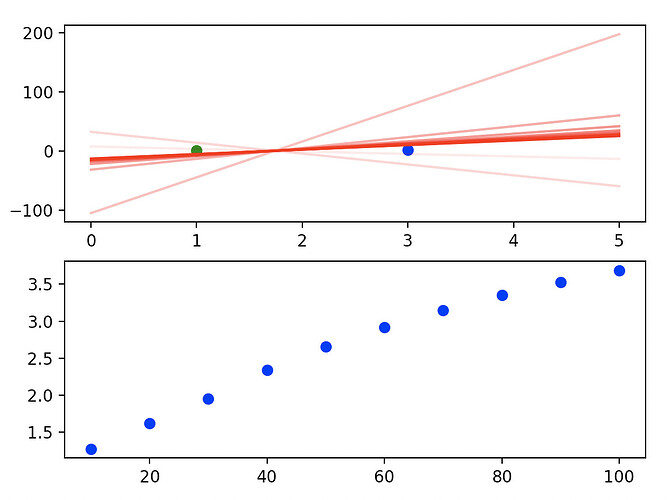
Output plot:
The top figure shows the output model, with a fainter line indicating an earlier epoch than a darker line. The bottom plot shows epoch no. against the sum of the absolute values of the weights.
I first thought to use weight decay because while the model was successfully classifying the points and the loss was decreasing with every epoch, the model with the lowest error should be the line which is a perpendicular bisector to the line connecting the centre of the two points. I wouldve thought that as the model continued to try and decrease the binary cross entropy error, it would tend towards becoming this perpendicular bisector. Instead, if you zoom into the plot it seems that the model is tending towards a line which is just barely classifying the points correctly (it seems to be rotating clockwise with each epoch) !
So I thought that this behaviour is occurring because the model is not being penalised for just increasing the strength of the weights to decrease the loss.
Introducing weight decay with lambda = 0.2 seems to just throw the model astray completely.
(new users cant input two images, so just set the weight decay parameter to 0.2 and you should see the problem)
Why ?
I guess the question I am asking is, given some model which correctly separates the data, there are two ways to decrease the loss, one is to increase the strength of the weights, while maintaining their relative ratio (so the actual gradient of the line is left unchanged), the other is to change the ratio of the weights such that the line tends towards being the perpendicular bisector of the line which connects the data point centres.
I thought L2 regularisation would prevent the model from just increasing the strengths of the weights blindly to decrease the loss, and instead try to tend towards the perpendicular bisector. Instead L2 loss fails to give me a model which separates the data points entirely… Why?