Why the gradient of feature passing into CrossEntroyLoss function is different from the theoretical value？

[CalmLife]

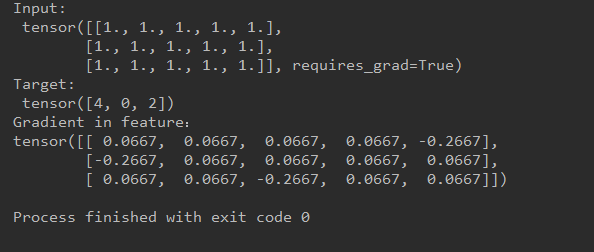
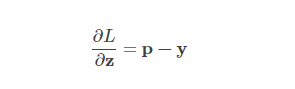Here is my code, it’s similar to official example.

import math
import torch
import torch.nn as nn
import torch.nn.functional as F


loss = nn.CrossEntropyLoss()
feature = torch.ones(3, 5, requires_grad=True)
target = torch.empty(3, dtype=torch.long).random_(5)

output_sm = F.log_softmax(feature, dim=1)
output_nll = F.nll_loss(output_sm, target)
output = output_nll
output.backward()

print("Input:\n", feature)
print("Target:\n", target)
print("Gradient in feature:\n", feature.grad)

The picture below is my results.

The result of theoretical deduction is as follow:

Partial derivative of L to z equals p - y

L represents loss function
z is the input feature
p is the output of softmax
y is the target
Regarding the detailed derivation of this formula, I am not here because it is easy to get.

What confused me is the experimental results do not match the theoretical values?
Can you give me some suggestion? Thank you!

[albanD]

What is the value you expect?
Given there is a log then softmax then nll then averaging. Plus the backward computations of each. I wouldn’t say it’s a trivial computation to do.

[CalmLife]

Thanks for your answer!
This is the formula.

p = [
     0.2 0.2  0.2 0.2 -0.8
-0.8 0.2  0.2 0.2 0.2
 0.2 0.2 -0.8 0.2 0.2
]

y = [4, 0, 2]

The values I expected as follows:
［
 0.2 0.2  0.2 0.2 -0.8
-0.8 0.2  0.2 0.2 0.2
 0.2 0.2 -0.8 0.2 0.2
]

[albanD]

Could you explain how you get dL/dz = p - y please?

[CalmLife]

Thank you! I have solved this problem. I did not divide by batches when caculating.
I will explain how I get dL/dz = p - y later.

[CalmLife]