I am following this PyTorch implementation of “Attention Is All You Need” and while initialising the Transformer class (here and here) the author sets the encoder_input_embedding.weight = decoder_input_embedding.weight = decoder_output_embedding.weight. However I can’t understand how is possible that this behaviour is not broken by optimiser.step(): what I mean is that, since this layers are in different position within the architecture, I would expect that the errors back-propagated would modify independently such layers. How does PyTorch handle this in its C++ backend?
Reusing the same layer (or generally any parameter) will capture its usage in the computation graph. The backward pass will then calculate the gradients for this layer using its grad outputs as well as forward activations. Each gradient will be accumulated in the .grad attribute of the corresponding parameter.
The optimizer does not have any visibility into the usage of the parameter it was getting and just updates each parameter using the stored .grad attribute and the step() formula.
Thanks for your response!
In other ways, you mean that by setting for instance encoder_input_embedding.weight = decoder_input_embedding.weight = decoder_output_embedding.weight the gradients accumulated with back propagation will be for each of the above layers the sum of the gradients accumulated of each individual layer?
Hi Alessandro,
With parameter sharing, the same tensor (more specifically: the same python object) will be used throughout the calculations in the computation graph. As @ptrblck has explained, the gradient from every branch in the computation graph will be accumulated in the grad attribute of the parameter.
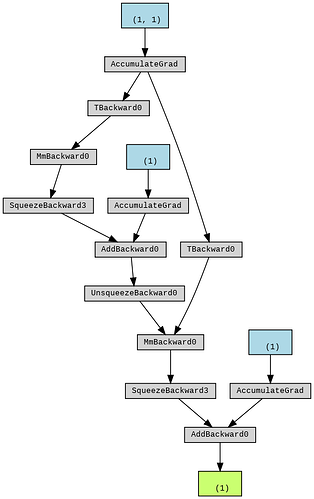
A simple example using torchviz helps understand this better -
fc1 = nn.Linear(1, 1)
fc2 = nn.Linear(1, 1)
# parameter initialisation
with torch.no_grad():
fc1.weight = fc2.weight = nn.Parameter(torch.tensor([[2.0]])) # weight sharing
fc1.bias = nn.Parameter(torch.tensor([2.0]))
fc2.bias = nn.Parameter(torch.tensor([4.0]))
inp = torch.tensor([1.0])
out = fc1(inp)
out = fc2(out)
make_dot(out).render("out", format="png")
gives:
As can be seen in the graph there’s one single node corresponding to the weight of both layers which ensures the calculated gradients match the theoretical values.
As for your question,
If this equivalence holds theoretically, it should be case in PyTorch as well.