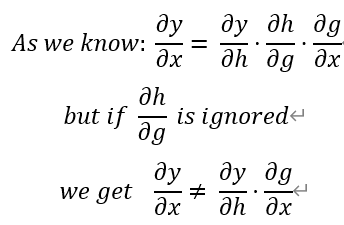Thanks for your help!
I’ve done the following simple experiment:
class Demo(nn.Module):
def __init__(self):
super(Demo, self).__init__()
self.layer1 = nn.Linear(1, 1, bias=False)
self.layer2 = nn.Linear(1, 1, bias=False)
self.layer3 = nn.Linear(1, 1, bias=False)
self.layer1.weight = nn.Parameter(torch.ones([1, 1]).float())
self.layer2.weight = nn.Parameter(torch.ones([1, 1]).float() * 2)
self.layer3.weight = nn.Parameter(torch.ones([1, 1]).float() * 3)
# self.layer1.register_forward_hook(lambda _, x_in, x_out: print('layer1', x_in, x_out))
# self.layer2.register_forward_hook(lambda _, x_in, x_out: print('layer2', x_in, x_out))
# self.layer3.register_forward_hook(lambda _, x_in, x_out: print('layer3', x_in, x_out))
self.layer1.register_backward_hook(lambda _, grad_in, grad_out: print('layer1', grad_in, grad_out))
self.layer2.register_backward_hook(lambda _, grad_in, grad_out: print('layer2', grad_in, grad_out))
self.layer3.register_backward_hook(lambda _, grad_in, grad_out: print('layer3', grad_in, grad_out))
# self.layer2.weight.requires_grad = False
def forward(self, x):
out = self.layer1(x)
out = self.layer2(out)
out = self.layer3(out)
return out
if __name__ == '__main__':
model = Demo()
optimizer = optim.SGD(params=model.parameters(), lr=0.1)
optimizer.zero_grad()
print(model.layer1.weight, model.layer2.weight, model.layer3.weight)
# for i in range(10):
x = torch.ones((1, 1))
out = model(x)
out.backward()
optimizer.step()
optimizer.zero_grad()
print(model.layer1.weight, model.layer2.weight, model.layer3.weight)
The result is:
# weights of linear layers
tensor([[1.]], requires_grad=True)
tensor([[2.]], requires_grad=True)
tensor([[3.]], requires_grad=True)
# for a linear layer: y = Wx
# gradients of backward_hook ((gradient for W, gradient for x), gradient for y)
layer3 (tensor([[3.]]), tensor([[2.]])) (tensor([[1.]]),)
layer2 (tensor([[6.]]), tensor([[3.]])) (tensor([[3.]]),)
layer1 (None, tensor([[6.]])) (tensor([[6.]]),)
# updated weights of linear layers
tensor([[0.4000]], requires_grad=True)
tensor([[1.7000]], requires_grad=True)
tensor([[2.8000]], requires_grad=True)
If we set self.layer2.weight.requires_grad = False, we’ll get:
tensor([[1.]], requires_grad=True)
tensor([[2.]])
tensor([[3.]], requires_grad=True)
layer3 (tensor([[3.]]), tensor([[2.]])) (tensor([[1.]]),)
layer2 (tensor([[6.]]), None) (tensor([[3.]]),)
layer1 (None, tensor([[6.]])) (tensor([[6.]]),)
tensor([[0.4000]], requires_grad=True)
tensor([[2.]])
tensor([[2.8000]], requires_grad=True)
We can see from this that setting the requires_grad flag to False will only set the gradient with respect to the weight of the layer to None, but the gradient wrt the x will be calculated and preserved for the shallower layer, which can be used for gradient descending correctly.