Clarity on default initialization in pytorch

1

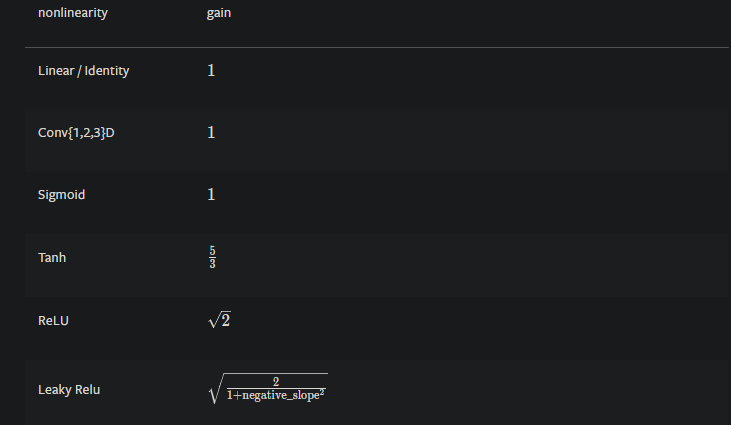
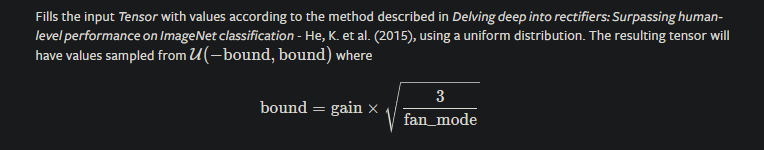According to the documentation for torch.nn, the default initialization uses a uniform distribution bounded by 1/sqrt(in_features), but this code appears to show the default initialization as Kaiming uniform. Am I correct in thinking these are not the same thing? And if so, perhaps the documentation can be updated?

Does anyone know the motivation for this choice of default? In particular, the code appears to define a negative slope for the subsequent nonlinearity of sqrt(5), whereas the default negative slope for a leaky relu in pytorch is 0.01. Also, does anyone know how this negative slope is actually incorporated into the initialization?

3 Likes
2

Hi,

Let me explain it step by step.

  1. Here is kaiming_uniform_.

    image
    image764×150 15.6 KB

    image
    image731×425 8.69 KB

    Where negative_slope=sqrt(5) so the gain=sqrt(2/6)=1/sqrt(3) for kaiming.
    If we replace this in bound formula, we get bound = [1/sqrt(3) ] * [sqrt(3/ fan_in)] which with a little simplification, it will be bound = 1/sqrt(fan_in) which can be represented by bound^2 = 1 / fan_in.

  2. In linear implementation code you referenced:
    image

    image
    image710×170 15.9 KB

So what we have here is that k= 1/in_feautres which in case of kaming it can be represented k=1/fan_in. Also, we want a boundary of [-sqrt(k), sqrt(k)] where k = bound^2= 1 / fan_in from step 1.

For simplcity, just replace sqrt(5) in gain formula then optain bound in kaiming_uniform_ and replace the bound as k in linear.

Edit: Add some related posts

  1. Kaiming init of conv and linear layers, why gain = sqrt(5) ¡ Issue #15314 ¡ pytorch/pytorch ¡ GitHub
  2. Why the default negative_slope for kaiming_uniform initialization of Convolution and Linear layers is √5?

Bests

3 Likes
3

Thanks so much for this very thorough explanation. So, if I understand correctly, this achieves what is described in the documentation (parameters drawn from uniform distribution bounded by 1/sqrt(in_features)), but in a kind of circuitous way. Although this approach uses the init.kaiming_uniform_ function, it is not actually Kaiming initialization (in the scenario where the subsequent nonlinearity is a ReLU). To get Kaiming initialization for a ReLU layer, one would need to re-initialize the weights using init.kaiming_uniform_ with nonlinearity set to ‘relu’. init Is that correct?

1 Like
4

You are welcome.
I think so, actually if you read the paper that introduces kaiming or he, its main advantage is that defines uniform distribution in the way that enables deep NNs with many layers to converge faster, so it is kind of super class of basic uniform as it can be obtained from kaiming_uniform. So, that is why I think if you define a small model using this approach, it won’t hurt the model’s performance and maybe because of this logic, it is the default init method(simplicity purposes without loosing performance).
But as you mentioned, logically gain for different activation functions are different and need to be incorporated.

1 Like
5

So what happened is that there were initializations in Torch7.
These have later been expressed as calls to kaiming_uniform.
But so there is not as much relation to the ideas of He’s paper as the use of the function might suggest.
At some point people thought changing the init were a good idea. But it seems that that’s something everyone wants to have done but noone wants to actually do.

Best regards

Thomas

2 Likes
6

Hi,

As i understand from this, linear layers are initialized by kaiming initialization. This initialization is supposed to give output tensors of mean 0 and std 1.
However, I noticed some contradicting stuff–

>>> k=nn.Linear(512,512)
>>> k1=torch.rand(512)
>>> out=k(k1)
>>> print(out.std(),out.mean())
tensor(0.3505, grad_fn=<StdBackward0>) tensor(0.0181, grad_fn=<MeanBackward0>)

Now, when i force kaiming initialization on the layer by –

 >>> nn.init.kaiming_uniform_(k.weight,mode='fan_in')
Parameter containing:
tensor([[-0.0134,  0.0247, -0.0817,  ..., -0.0807, -0.0330, -0.0881],
        [-0.0641,  0.0447,  0.0645,  ...,  0.1048, -0.0307,  0.0989],
        [ 0.0745, -0.0076,  0.0161,  ...,  0.0252,  0.0285, -0.0527],
        ...,
        [ 0.0190, -0.0529, -0.0549,  ..., -0.0369,  0.0331,  0.0136],
        [ 0.0347,  0.0516,  0.0108,  ..., -0.0772,  0.0027,  0.0584],
        [-0.0236,  0.0565,  0.0082,  ...,  0.0717, -0.0619, -0.0772]],
       requires_grad=True)
>>> out=k(k1)
>>> print(out.std(),out.mean())
tensor(0.8420, grad_fn=<StdBackward0>) tensor(-0.0287, grad_fn=<MeanBackward0>)

I get the tensors nearing the actual mean and std values. What am i missing here?
Thanks :slight_smile:

7

So the thing we discussed above is that while the default init is expressed as kaiming init times some gain factor, it is not kaiming init, as the gain factor is “bogus” w.r.t. kaiming init and the activation function and only serves to reproduce ancient behaviour.
Happily, @Kushaj started work on it.

2 Likes