(continue …)
But it should back-propagate like this:
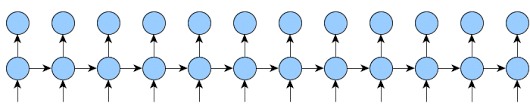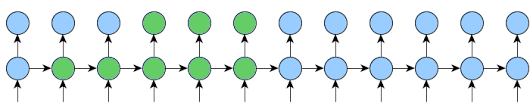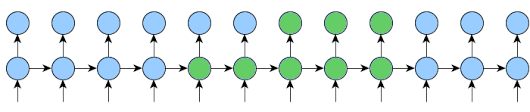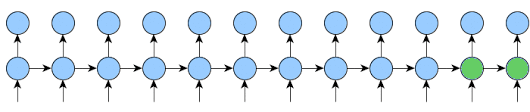
It’s easy to implement the second one by changing few lines in train function.
def train(self, input_sequence, init_state):
states = [(None, init_state)]
outputs = []
targets = []
for i, (inp, target) in enumerate(input_sequence):
state = states[-1][1].detach()
state.requires_grad=True
output, new_state = self.one_step_module(inp, state)
outputs.append(output)
targets.append(target)
while len(outputs) > self.k1:
# Delete stuff that is too old
del outputs[0]
del targets[0]
states.append((state, new_state))
while len(states) > self.k2:
# Delete stuff that is too old
del states[0]
if (i+1)%self.k1 == 0:
# loss = self.loss_module(output, target)
optimizer.zero_grad()
# backprop last module (keep graph only if they ever overlap)
start = time.time()
# loss.backward(retain_graph=self.retain_graph)
for j in range(self.k2-1):
if j < self.k1:
loss = self.loss_module(outputs[-j-1], targets[-j-1])
loss.backward(retain_graph=True)
# if we get all the way back to the "init_state", stop
if states[-j-2][0] is None:
break
curr_grad = states[-j-1][0].grad
states[-j-2][1].backward(curr_grad, retain_graph=self.retain_graph)
print("bw: {}".format(time.time()-start))
optimizer.step()
I think it may also be possible to implement it without outputs and targets lists.
I splitted my post, because as a new user i can post only one image per post.