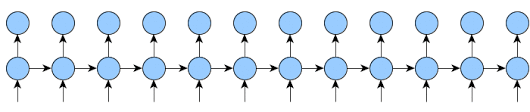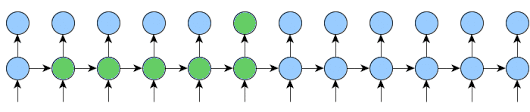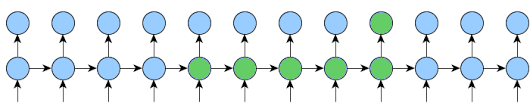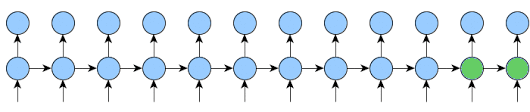
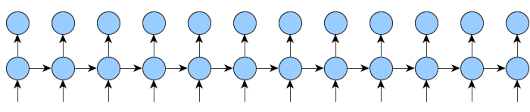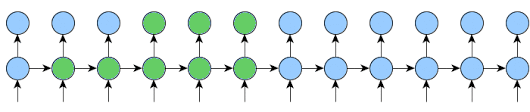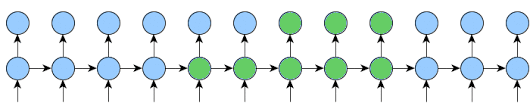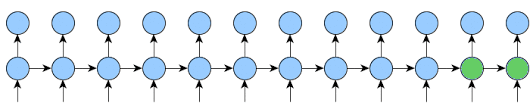
Here is an implementation that will work for any k1 and k2 and will reduce memory usage as much as possible.
If k2 is not huge and the one_step_module is relatively big, the slowdown of doing multiple backward should be negligible.
The code is not super clean and has been tested only against current master branch (where Variable and Tensor are merged) so you might need slight modifications if you use 0.3.
Hope this helps.
class TBPTT():
def __init__(self, one_step_module, loss_module, k1, k2, optimizer):
self.one_step_module = one_step_module
self.loss_module = loss_module
self.k1 = k1
self.k2 = k2
self.retain_graph = k1 < k2
# You can also remove all the optimizer code here, and the
# train function will just accumulate all the gradients in
# one_step_module parameters
self.optimizer = optimizer
def train(self, input_sequence, init_state):
states = [(None, init_state)]
for j, (inp, target) in enumerate(input_sequence):
state = states[-1][1].detach()
state.requires_grad=True
output, new_state = self.one_step_module(inp, state)
states.append((state, new_state))
while len(states) > self.k2:
# Delete stuff that is too old
del states[0]
if (j+1)%self.k1 == 0:
loss = self.loss_module(output, target)
optimizer.zero_grad()
# backprop last module (keep graph only if they ever overlap)
start = time.time()
loss.backward(retain_graph=self.retain_graph)
for i in range(self.k2-1):
# if we get all the way back to the "init_state", stop
if states[-i-2][0] is None:
break
curr_grad = states[-i-1][0].grad
states[-i-2][1].backward(curr_grad, retain_graph=self.retain_graph)
print("bw: {}".format(time.time()-start))
optimizer.step()
seq_len = 20
layer_size = 50
idx = 0
class MyMod(nn.Module):
def __init__(self):
super(MyMod, self).__init__()
self.lin = nn.Linear(2*layer_size, 2*layer_size)
def forward(self, inp, state):
global idx
full_out = self.lin(torch.cat([inp, state], 1))
# out, new_state = full_out.chunk(2, dim=1)
out = full_out.narrow(1, 0, layer_size)
new_state = full_out.narrow(1, layer_size, layer_size)
def get_pr(idx_val):
def pr(*args):
print("doing backward {}".format(idx_val))
return pr
new_state.register_hook(get_pr(idx))
out.register_hook(get_pr(idx))
print("doing fw {}".format(idx))
idx += 1
return out, new_state
one_step_module = MyMod()
loss_module = nn.MSELoss()
input_sequence = [(torch.rand(200, layer_size), torch.rand(200, layer_size))] * seq_len
optimizer = torch.optim.SGD(one_step_module.parameters(), lr=1e-3)
runner = TBPTT(one_step_module, loss_module, 5, 7, optimizer)
runner.train(input_sequence, torch.zeros(200, layer_size))
print("done")