I want to test my tensor to see if I have to call .detach() on them. Any way of testing that?
Hi,
You can check if they have the requires_grad field to True. That would mean that some leaf tensor need gradients through them to compute their gradients.
Thank you so much! Why it’s not in the doc? Tensor Attributes — PyTorch 2.1 documentation
HI,
It is mentioned in the tensor part.
But indeed this should be added as well as is_leaf (that will tell you if a tensor is a leaf tensor).
from my understanding a leaf is a tensor witch don’t require gradiant.
so not requires_grad == is_leaf is always true
But I really not understand what is really a leaf.
to compute the gradiant you generate a tree? what are the node in the tree witch are not leaf?
A leaf tensor is a tensor with no parent in the graph. If it does not require grad, then it never has parents and is always a leaf, if it requires grad, it is a leaf only if it was created by the user (not the result of an op). When running the backward pass, the gradients are accumulated in all the leaf tensors that require gradients.
related question. Why aren’t cloned vectors leaf nodes (specially if they are clones of leaf nodes):
import torch
w = torch.tensor([2.0], requires_grad=True)
w1 = torch.tensor([2.0], requires_grad=False)
w_clone = w.clone()
print(w)
print(w.is_leaf)
print(w1.is_leaf)
print(w_clone)
print(w_clone is w)
print(w_clone == w)
print(w_clone.is_leaf)
tensor([2.], requires_grad=True)
'''
output:
'''
True
True
tensor([2.], grad_fn=<CloneBackward>)
False
tensor([True])
False
what does it even mean to do a backward pass/differentiation of a cloned operation?
The backward of a clone is just a clone of the gradients.
All (almost) of pytorch operations are differentiable. And you can compute gradient through them.
If you want to break the graph you should use .detach().
Really? Including .clone()? I’ve seen it my graph and thought that was super strange (related question: Why is the clone operation part of the computation graph? Is it even differentiable?).
#%%
## Q:
import torch
from torchviz import make_dot
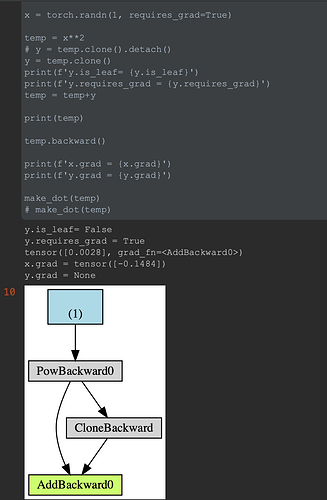
x = torch.randn(1, requires_grad=True)
temp = x**2
# y = temp.clone().detach()
y = temp.clone()
print(f'y.is_leaf= {y.is_leaf}')
print(f'y.requires_grad = {y.requires_grad}')
temp = temp+y
print(temp)
temp.backward()
print(f'x.grad = {x.grad}')
print(f'y.grad = {y.grad}')
make_dot(temp)
# make_dot(temp)
I’m really curious! What are examples of an operations that are not differentiable?
Usually operations that return indices like argmax. Or any function that works with integer values (index is not differentiable wrt the indices for example, only the values).
I thought that was correct but I tried running some code and the result of exponentiation results in the dummy loss being a leaf, which I thought was super bizarre. Is there anything wrong with my code? shouldn’t l_y NOT be a leaf?
import torch
from torchviz import make_dot
lst = []
lst2 = lst
print('-- lst vs lst2')
print(lst is lst2)
lst.append(2)
print(f'lst={lst} vs lst2={lst2}')
x = torch.tensor([2.0],requires_grad=False)
xx = x
print('-- x vs xx')
print(f'xx == x = {xx == x}')
print(f'xx is x = {xx is x}')
xx.fill_(4.0)
print(f'x = {x}')
print(f'xx = {xx}')
x = torch.tensor([2.0],requires_grad=False)
y = x**2
l_y = (y - x + 3)**3 + 123
print('\n-- x vs y')
print(f'y = {y}')
print(f'y == x = {y==x}')
print(f'y is x = {y is x}')
print(f'y.is_leaf = {y.is_leaf}')
print(f'l_y.is_leaf = {l_y.is_leaf}')
y.fill_(3.0)
print(f'x = {x}')
print(f'y = {y}')
print(f'x.is_leaf = {x.is_leaf}')
print(f'y.is_leaf = {y.is_leaf}')
print(f'l_y.is_leaf = {l_y.is_leaf}')
result:
-- lst vs lst2
True
lst=[2] vs lst2=[2]
-- x vs xx
xx == x = tensor([True])
xx is x = True
x = tensor([4.])
xx = tensor([4.])
-- x vs y
y = tensor([4.])
y == x = tensor([False])
y is x = False
y.is_leaf = True
l_y.is_leaf = True
x = tensor([2.])
y = tensor([3.])
x.is_leaf = True
y.is_leaf = True
l_y.is_leaf = True
I doubt its a bug in pytorch but I can’t see what I did wrong…or is my expectation wrong?
A leaf is a Tensor with no gradient history. You need to keep in mind that Tensors that do not require gradients, since we don’t track their history, they are always leafs.
So when you create x = torch.tensor([2.0],requires_grad=False), it is a leaf because it has no history. But when you use it in y = x**2, since x does not require gradients, we do not track the operation, and y does not require gradient and has no history. So y is a leaf as well. Same thing for the computation of your loss.
Ah! I see. That makes so much sense.
I didn’t even realize I had it’s requires_grad flag set to false X’D
I confirmed what you said and its true, it was fixed after changing that flag:
print('-- what is a leaf?')
y_clone = y.clone()
print(f'y.is_leaf = {y_clone.is_leaf}')
x = torch.tensor([2.0],requires_grad=True)
lx = (x - 3)**2
print(f'x.is_leaf = {x.is_leaf}')
print(f'lx.is_leaf = {lx.is_leaf}')
result:
-- is y_clone an leaf
y.is_leaf = True
x.is_leaf = True
lx.is_leaf = False
Thanks! Again your a savior ![]()