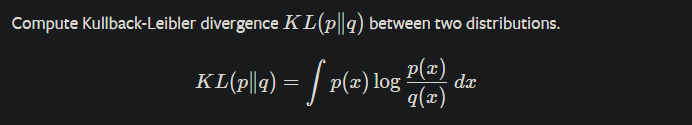KL-divergence between two multivariate gaussian

Rojin · August 9, 2019, 7:11pm

I have two multivariate Gaussian distributions that I would like to calculate the kl divergence between them. each is defined with a vector of mu and a vector of variance (similar to VAE mu and sigma layer). What is the best way to calculate the KL between the two? Is this even doable? because I do not have the covariance matrix. If that is not doable, what if I take samples from both distributions and calculate the KL between the samplings? is that the right way of doing this? is there any build-in function for any of these calculations?

Nikronic · August 9, 2019, 7:56pm

Hi,

Yes, this is the correct approach.
Just be aware that the input a must should contain log-probabilities and the target b should contain probability.

github.com

pytorch/pytorch/blob/35fed93b1ef05175143f883c6f89f06c6dd9429b/aten/src/ATen/native/Loss.cpp#L71


      
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor margin_ranking_loss(const Tensor& input1, const Tensor& input2, const Tensor& target, double margin, int64_t reduction) {
            auto output =  (-target * (input1 - input2) + margin).clamp_min_(0);
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor kl_div(const Tensor& input, const Tensor& target, int64_t reduction) {
            auto zeros = at::zeros_like(target);
            auto output_pos = target * (at::log(target) - input);
            auto output = at::where(target > 0, output_pos, zeros);
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor kl_div_backward_cpu(const Tensor& grad, const Tensor& input, const Tensor& target, int64_t reduction) {
            auto grad_input = at::zeros_like(input);
            auto grad_expand = grad.expand_as(input);
            AT_DISPATCH_FLOATING_TYPES(input.scalar_type(), "kl_div_backward_cpu", [&]() {
              at::CPU_tensor_apply3<scalar_t, scalar_t, scalar_t>(
                  grad_input,

https://pytorch.org/docs/stable/nn.functional.html?highlight=kl_div#kl-div

By the way, PyTorch use this approach:

https://pytorch.org/docs/stable/distributions.html?highlight=kl_div#torch.distributions.kl.kl_divergence

Good luck
Nik

Rojin · August 13, 2019, 11:52pm

Thanks Nick for your input. I should restate my question. I have two multi-variate distributions each defined with “n” mu and sigma. Now I would like to do a KL between these two. Any idea how that can be done?

zhl515 · August 14, 2019, 6:42am

You can sample x1 and x2 from 𝑝1(𝑥|𝜇1,Σ1) and 𝑝2(𝑥|𝜇2,Σ2) respectively, then compute KL divergence using torch.nn.functional.kl_div(x1, x2).

Rojin · August 14, 2019, 4:33pm

As @Nikronic mentioned the kl_div requires a to be log-probabilities and the target b to be probability. correct me if I’m wrong, but I think sampling from the two distributions is not going to give log-probabilities and probabilities

Rojin · August 16, 2019, 12:02am

any suggestion? I don’t think that what you said can be used for sampling layer

Nikronic · August 16, 2019, 12:13am

@Rojin
Actually, I have never used distribution class but based on docs, in this situation you just need to pass them directly to kl_div from distribution if the aforementioned distributions are obtained from Distribution subclasses or you have registered your own.

Please refer to this links for more information:

well, you know, my name is Nik, somehow abbreviated of Nikan (a Persian name)

Bests

Rojin · August 16, 2019, 12:44am

Hey Nikan!

Yeah I realized that from your last name!

Sorry if I’m restating my question ( I modified it a couple of times at the top lol) and probably repeating your answer, I’m kinda new to the KL implementation in pytorch, so I really appreciate your help.

My question is :
I have two VAEs, each with a mu and standard deviation layers. Now I would like to calculate the KL between these two VAEs using either the mu and sds, or the sampling layers. This sounds to me like a multivariate gaussian KL divergence problem, so I looked at the formula and I noticed that I actually need the covariance matrix of q (if we assume that KL(p||q) ). And as far as I know there is no way to calculate the covariance in this case, am I correct?

@zhl515 suggested to directly calculate the KL between the two sampling layers as you said before using the bellow function, but as you said this requires probabilities which I do not have, so I think the following function cannot be used on the sampling layers, is that right? :

 torch.nn.functional.kl_div(p, q).

And based on your last comment, you are suggesting to register the distribution, and then use

torch.distributions.kl.kl_divergence(p, q)

The only problem is that in order to register the distribution I need to have the covariance matrix, and I can’t obtain that because I only have mu and std. It makes me think whether that is a possible thing to do at all in neural network. In the VAE paper they don’t have that problem because the are assuming that q has mean 0 and covariance I

Thank you!

zhl515 · August 16, 2019, 7:07am

You said you can’t obtain covariance matrix. In VAE paper, the author assume the true (but intractable) posterior takes on a approximate Gaussian form with an approximately diagonal covariance. So just place the std on diagonal of convariance matrix, and other elements of matrix are zeros.

zhl515 · August 16, 2019, 7:16am

Now you can compute KL-divargence of two multivariate Gaussians directly from the below formula:
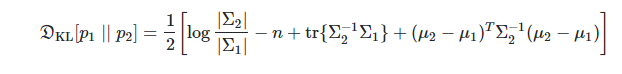
1565939371(1)

Rojin · August 16, 2019, 7:31am

Thank you that solves the problem

shivangi · October 6, 2019, 6:02pm

Hey @Rojin
Could you share how you computed the KL-divergence? I am also trying to achieve the same

LiUzHiAn · December 11, 2019, 9:31am

Hi, @zhl515.

Thanks for your solution and I’ve coded as you post, like this:

def kl_divergence(mu1, mu2, sigma_1, sigma_2):
	sigma_diag_1 = np.eye(sigma_1.shape[0]) * sigma_1
	sigma_diag_2 = np.eye(sigma_2.shape[0]) * sigma_2

	sigma_diag_2_inv = np.linalg.inv(sigma_diag_2)

	kl = 0.5 * (np.log(np.linalg.det(sigma_diag_2) / np.linalg.det(sigma_diag_2))
				- mu1.shape[0] + np.trace(np.matmul(sigma_diag_2_inv, sigma_diag_1))
				+ np.matmul(np.matmul(np.transpose(mu2 - mu1), sigma_diag_2_inv), (mu2 - mu1))
				)

	return kl

But I have another problem that I cannot call it in a “vectorized” way, or say, I don’t know how to let my code support batch operation in Pytorch. For instance, I have a tensor mu_1 with shape [batch_size,n] and another tensor mu_2 with shape [batch_size,n]. The variance tensors are same with mu. The n here is the dimensions of Gaussian distribution. How can I calculate kl loss for each instance without using for-loop ?

Any ideas? thx

NILOIDE · February 4, 2020, 1:42pm

Check this thread.
torch.diag_embed() should do the trick.

hf_Morii · November 9, 2020, 8:59am

hi i don’t know much about the meaning of mu1 mu2 sigma_1 and sigma_2

Dane_Mitrev · November 9, 2020, 8:49pm

I am not sure I understand fully your question, but IMO if you have mu1, mu2, sigma_1, sigma_2, why not create two instances of MultivariateNormal using diagonal covariance matrices?

# mu1 [batch_size, n]
# assuming that sigma1 is [batch_size, n] also
cov1 = torch.stack([torch.diag(sigma) for sigma in torch.exp(sigma_1)])
mvn1 = MultivariateNormal(mu1, cov1)

...
# similarly for mvn2

MultivariateNormal will interpret the batch_size as the batch dimension automatically thus mvn1 would have:

batch_shape = batch_size
event_shape = n
sample_shape = ()

when you sample it will take into consideration the batch_shape.

You can compute kl (mvn1, mvn2) using the Pytorch’s implementation.

I hope this can help.

hf_Morii · November 10, 2020, 1:50pm

This is really helpful!
Thanks a lot.

muammar · September 12, 2021, 12:13am

Is this formula applicable to any arbitrary distribution? e.g., non-Gaussian?

banikr · November 15, 2022, 12:32am

The cov-variance matrix must be positive definite.
Any idea how to turn a diagonal matrix with zero non-diagonal elements into a positive definite matrix?

The output comes from an FC+BN+ReLU layer.
then I can turn it into a diagonal by:

cov_var_diag = torch.diag_embed(output)
cov_var_spd = cov_var @ cov_var.mT + 1e-6 # this actually makes symmetric positive definite and didn't work
q = torch.distributions.multivariate_normal.MultivariateNormal(loc=mu, covariance_matrix=cov_var_spd)

Also looked into Cholesky decomposition into lower triangular matrix as scale_tril attribute in MVN function, but that also didn’t end well.