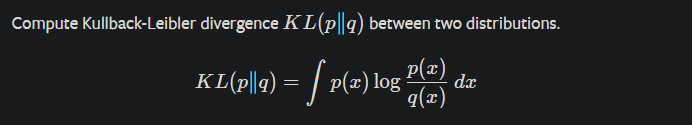KL-divergence between two multivariate gaussian

Nikronic · August 9, 2019, 7:56pm

Hi,

Yes, this is the correct approach.
Just be aware that the input a must should contain log-probabilities and the target b should contain probability.

github.com

pytorch/pytorch/blob/35fed93b1ef05175143f883c6f89f06c6dd9429b/aten/src/ATen/native/Loss.cpp#L71


      
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor margin_ranking_loss(const Tensor& input1, const Tensor& input2, const Tensor& target, double margin, int64_t reduction) {
            auto output =  (-target * (input1 - input2) + margin).clamp_min_(0);
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor kl_div(const Tensor& input, const Tensor& target, int64_t reduction) {
            auto zeros = at::zeros_like(target);
            auto output_pos = target * (at::log(target) - input);
            auto output = at::where(target > 0, output_pos, zeros);
            return apply_loss_reduction(output, reduction);
          }
          
          Tensor kl_div_backward_cpu(const Tensor& grad, const Tensor& input, const Tensor& target, int64_t reduction) {
            auto grad_input = at::zeros_like(input);
            auto grad_expand = grad.expand_as(input);
            AT_DISPATCH_FLOATING_TYPES(input.scalar_type(), "kl_div_backward_cpu", [&]() {
              at::CPU_tensor_apply3<scalar_t, scalar_t, scalar_t>(
                  grad_input,

https://pytorch.org/docs/stable/nn.functional.html?highlight=kl_div#kl-div

By the way, PyTorch use this approach:

https://pytorch.org/docs/stable/distributions.html?highlight=kl_div#torch.distributions.kl.kl_divergence

Good luck
Nik