Hey
I am having issues with the LSTM function in pytorch. I am using an LSTM neural network to forecast a certain value. The input is multidimensional (multiple features) and the output should be one dimensional (only one feature that needs to be forecasted). I want to forecast something 1-6 timesteps in advance. I want to use multi timestep input as well. Now I have to different ways of achieving this but neither of them seem to work.
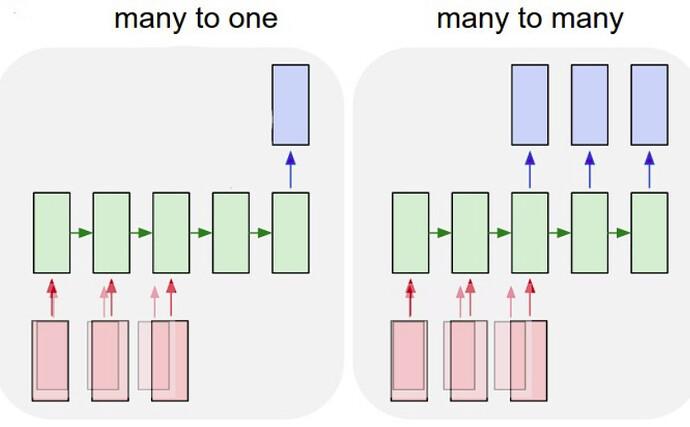
The first one is making 6 different many-to-one networks each forecasting another timestep 1-6h in advance, but still using the recurrent structure (see picture) when forecasting multiple time steps ahead (so not just shifting the target data by 1-6 hours). Another option would be a many to many neural network, this would work fine as well I think. (also see picture)
My input now looks like: where first the different parameters at the same timestep are grouped and then further each time all the timesteps we want to use in the forecast are grouped (look back)
tensor([[[-0.2800, -0.6381, -0.1033, -0.4941, 0.0016],
[-0.3159, 0.1378, -0.1010, -0.4529, 0.0016],
[-0.2800, 0.1378, -0.0963, -0.4706, 0.1150],
…,
[-0.5673, -0.2149, -0.0598, -0.4000, 0.2850],
[-0.3518, -0.4265, -0.0669, -0.3646, 0.3417],
[-0.2440, -0.0738, -0.0657, -0.3823, 0.2283]],
[[-0.3159, 0.1378, -0.1010, -0.4529, 0.0016],
[-0.2800, 0.1378, -0.0963, -0.4706, 0.1150],
[-0.7469, 0.1731, -0.0845, -0.4176, 0.3417],
...,
[-0.3518, -0.4265, -0.0669, -0.3646, 0.3417],
[-0.2440, -0.0738, -0.0657, -0.3823, 0.2283],
[-0.1722, -0.5323, -0.0610, -0.4117, 0.2283]],
[[-0.2800, 0.1378, -0.0963, -0.4706, 0.1150],
[-0.7469, 0.1731, -0.0845, -0.4176, 0.3417],
[-0.7829, -0.4265, -0.0692, -0.4176, 0.4550],
...,
[-0.2440, -0.0738, -0.0657, -0.3823, 0.2283],
[-0.1722, -0.5323, -0.0610, -0.4117, 0.2283],
[-0.1363, -0.8850, -0.0669, -0.4294, 0.1150]],
...,
[[-0.3518, 0.2083, -0.1386, 0.8479, -0.1684],
[-0.3518, 0.4552, -0.1398, 0.9480, 0.0016],
[-0.2800, -0.4265, -0.1398, 0.9126, 0.0583],
...,
[-1.0343, -0.1443, -0.1433, 0.8479, 0.0016],
[-0.8906, 0.3847, -0.1445, 1.0304, -0.2251],
[-0.7829, -0.0385, -0.1433, 1.0127, -0.1117]],
[[-0.3518, 0.4552, -0.1398, 0.9480, 0.0016],
[-0.2800, -0.4265, -0.1398, 0.9126, 0.0583],
[-0.4596, -0.9202, -0.1410, 0.8479, 0.1150],
...,
[-0.8906, 0.3847, -0.1445, 1.0304, -0.2251],
[-0.7829, -0.0385, -0.1433, 1.0127, -0.1117],
[-0.8547, 0.2436, -0.1422, 0.9715, -0.0550]],
[[-0.2800, -0.4265, -0.1398, 0.9126, 0.0583],
[-0.4596, -0.9202, -0.1410, 0.8479, 0.1150],
[-0.6392, -0.5323, -0.1422, 0.8655, 0.0016],
...,
[-0.7829, -0.0385, -0.1433, 1.0127, -0.1117],
[-0.8547, 0.2436, -0.1422, 0.9715, -0.0550],
[-0.9984, -0.0033, -0.1422, 0.8597, 0.0583]]])
And the output looks like, where the different timesteps 1-6h in advance are grouped. I can change this easily.
tensor([[[ -7.],
[ -9.],
[-11.],
[-13.],
[-13.]],
[[ -9.],
[-11.],
[-13.],
[-13.],
[-10.]],
[[-11.],
[-13.],
[-13.],
[-10.],
[ -9.]],
...,
[[-12.],
[-10.],
[-10.],
[-10.],
[ -9.]],
[[-10.],
[-10.],
[-10.],
[ -9.],
[ -8.]],
[[-10.],
[-10.],
[ -9.],
[ -8.],
[-10.]]])
Now I have no idea how to use the LSTM structure to do multi timesteps forecasting. The output layer should be linear.
The batch size does not really matter to me, I think it can be one for now.