What is the typical scale of model parameters?

1

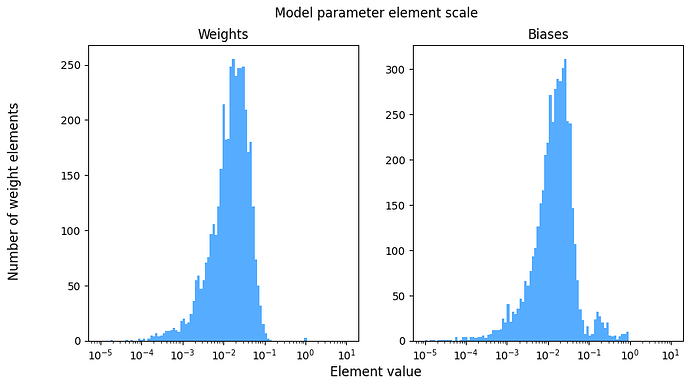
I think my model’s parameters are very small. The histgrams below shows that most of the parameters are < 0.1. I am worried that this makes my model sensitive to floating point precision.
My model is a very typical autoregressive generative model with 12 decoder-only transformer layers (almost identical to GPT-2)
Is the scale of my model’s parameters acceptable?

image
image899×505 20.8 KB

You can create these histgrams with your own model parameters with the code below.
Can anyone share your model’s parameter scale?

import numpy as np
import torch
import matplotlib.pyplot as plt

def visualize_parameter_scale(state_dict_path:str, n_shown:int=1e5)->None:
    """Visualize your model's parameter scale with histgrams.
    Args:
        state_dict_path (str): Path to a state dict that stores model parameters.
        n_shown (int, optional): If specified, the given number of parameters are randomly sampled for plot.
            The default is 100,000. If you want to plot everyhting, set this to None.
    Returns:
        None
    """
    # Load state dict
    sd = torch.load(state_dict_path, map_location="cpu")
    # Collect params
    weights = []
    biases = []
    for k, v in sd.items():
        f = v.flatten().numpy()
        if ".weight" in k:
            weights.append(f)
        elif ".bias" in k:
            biases.append(f)
    weights = np.hstack(weights)
    biases = np.hstack(biases)
    if n_shown is not None:
        n_shown = int(n_shown)
        weights = np.random.choice(weights, n_shown)
        biases = np.random.choice(biases, n_shown)
    # plot
    fig, axes = plt.subplots(1, 2, figsize=(10, 5))
    axes[0].hist(x=weights, bins=np.logspace(-5, 1, 100), color='dodgerblue', alpha=0.75)
    axes[0].set_xscale('log')
    axes[0].set_title("Weights")
    axes[1].hist(x=biases, bins=np.logspace(-5, 1, 100), color='dodgerblue', alpha=0.75)
    axes[1].set_xscale('log')
    axes[1].set_title("Biases")
    fig.supxlabel('Element value')
    fig.supylabel('Number of weight elements')
    fig.suptitle("Model parameter element scale")
    plt.show()
2

Hi @YuA,

Floating point round error shouldn’t be an issue at 1e-4, and are common around 1e-7 (for single precision).

Also, a more efficient method to get all the parameters can be found below,

import torch
from torchvision import models

net = models.resnet18() #example model

params = torch.cat([p.view(-1) for p in net.parameters()], dim=0)

print(params.shape) #returns torch.Size([11689512])
1 Like
3

Hi Alpha (and Yu)!

This isn’t really right. Floating-point numbers with smaller magnitudes
aren’t any more subject to round-off error. (A single-precision float
does start to underflow at around 1.e-38, but this is underflow,
rather than round-off error.)

If you did successful computations with a bunch of floating-point
numbers all with magnitude of order one, the same computations
would work just fine if you were to first multiply all the numbers by,
say, 1.e-20. (In some sense, this is the whole point of floating-point
arithmetic.)

Best.

K. Frank

2 Likes
4

You made it very clear for me. Thank you very much Frank.
I am now sure that the parameter scale of my model is not a problem.
However, I still cannot solve the problem that I am facing, apparently related to the numerical accuracy. I created a new topic:

I will appreciate it very much if you can give me more insights into this problem.
Thank you very much again for your help.

5

Thank you for your answer!