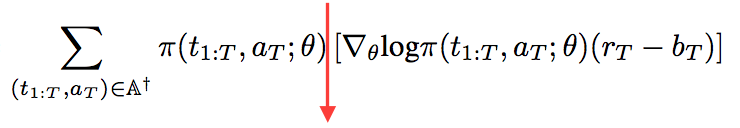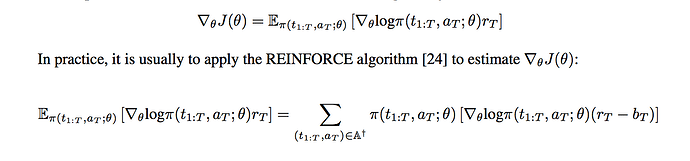Hello everyone!
I’m trying to perform this gradient update directly, without computing loss.
![]()
But I simply haven’t seen any ways I can achieve this. Looks like first I need some function to compute the gradient of policy, and then somehow feed it to the backward function.
I think you should look at this topic explaining the tensor.reinforce method:
If the action is the result of a sampling, calling action.reinforce(r) acts as a policy gradient.
You can find a code example of implementation here:
Or you can just have
loss = samples_logprob * (reward - baseline)
(logprob is the output of the network, and reward and baseline are leaf variables)
If you do backward, the gradient backpropogated is equivalent to the policy gradient.
hi everyone, I am new to pytorch, my question is a litter different from @Eddie_Li,
is there any way to change grad after backward?
I mean loss = right side of the red line
After backward, can I do pai(theta) * loss.grad, and then optimizer.step() ?
Is that way work?
the right side of your red line looks rather the gradient of your loss?
Your loss would be something like
loss = - torch.sum(torch.log( policy(state) * (reward - baseline)))
then you compute the gradient of this loss with respect to all the parameters/variables that requires a gradient in your code by calling:
loss.backward()
and if you created, before the training loop, an optimizer associated to your policy like this:
optim_policy = optim.MyOptimizer( policy.parameters(), lr = wathever)
you can update your optimizer simply like this, after each backward call of your loss:
optim_policy.step()
the parameters of your policy (theta) will be updated with the gradient of your loss in order to minimize your loss.
Thanks for your help, but my question is a little different
In my formula A* is a set of all possible episodes
when I update parameters , I want something like
policy * grad of loss
or in other words
(p1loss(p1) + …+pNloss(pN)) , where p1+…+pN = 1
your solution is
(loss(p1)+…+loss(pN)) / N
I want to change grad between loss.backward() and optim_policy.step()
I tried loss.grad() but it is None 
Then, I am not sure to understand your question… You want to use the policy as weights for the gradient update ? that way, you should re-write your loss:
weighted_loss = p1*loss(p1) + .. + pn*loss(pn)
weighted_loss.backward()
optimizer.step()
policy is the weight of loss.grad, not the weight of loss itself.
taken as a scalar quantity (that’s what I mean by weight) it’s just the same: grad(w*x) = w*grad(x)
you just have to make sure you are not using it as a variable of the tree (using pi.detach() should do it)
Thanks a lot, it looks like detach() is what I want:blush:
I am doing a similar example to this and I am having trouble defining the “baseline” variable. I tried
base_line=Variable(Variable(torch.ones(2), requires_grad=True))
base_line=base_line[0]
and get the error “RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn”. I only have one baseline value, could you suggest a way to define this varieble?
Generally, the baseline is an approximation of the expected reward, that does not depend on the policy parameters (so it does not affect the direction of the gradient).
This approximation can be the output of another network that takes the state as input and returns a value, and you minimize the distance between the observed rewards and the predicted values. Then, over a rollout, you predict the values of all states with this model, and remove the values from the rewards:
# policy = Policy() # the network that computes the prob of your actions
# value = Value() # the network that predicts the rewards
loss = - torch.sum( torch.log(policy(states)) * (rewards - values(states) )
That’s the idea of the actor critic for policy gradient. You have a full example here: https://github.com/pytorch/examples/blob/master/reinforcement_learning/actor_critic.py
If your rollout is long enough, the sum of rewards approximates Q and the sum of values approximates V, so the term (rewards - values) approximate the advantage (Q-V) which is a non-biased estimator of the temporal difference (hence the name advantage-actor-critic).
Just a quick question. The log probabilities are negative. If the rewards are positive, then the product with high rewards will make negative log prob values even lower (and loss even bigger)? Isn’t it opposite to what we need? Or the rewards should be negative? Did I miss anything?
the log_prob*advantage quantity is the objective to maximize. If a reward is negative, then having a large negative log_probs gives a large objective. At the opposite, if a reward is positive, then having small negative log_probs (close to 0) maximizes the objective.
With Pytorch, we need a loss to minimize, so we take loss=-objective.
Hello, I implemented the loss like you said, and it works.
However, why doesn’t it have the opposite sign? Because the given gradient is actually for gradient ascent.
@alexis-jacq I think your line is wrong
loss = - torch.sum(torch.log( policy(state) * (reward - baseline)))
Shouldn’t the reward - baseline be outside the log(policy(state))?
I am thinking the same thing… if reward - baseline = 0 then this will give log(0)
I had similar question, with 0 reward the loss will be equal to 0 and if the reward its 1 or greater the loss will be some positive value. shouldn’t it be opposite, getting reward 0 should have higher loss and getting reward 1 should have lower loss when inplementing REINFORCE in pytorch?
This “loss” is actually not a proper loss.
The negative loss (the objective) is actually
int p(x) r(x) dx
where p(x) is the prob distribution and r(x) the reward function.
So if the expectation of r(x) gets higher, your objective gets higher (this is what you want).
Now, we derive the gradient of that wrt some parameter theta (that i omitted for simplicity) of the distribution and we obtain that the gradient is:
grad obj(theta) = grad int p(x;theta) r(x) dx
which we simplify into
grad obj(theta) = int grad (log p(x;theta)) p(x;theta) r(x;theta) dx
(this comes from the fact that grad f(x) = grad (log f(x)) f(x) if f(x) > 0).
If you take monte carlo samples, you get that
grad log p(x;theta) r
if an estimator (i.e. converges with large number of samples) to grad obj(theta) when x is sampled according to p(x;theta).
From there, people do the hack of saying that log p(x;theta) r is your objective BUT it’s not true (programatically it is how we will write it but you should not look at its value).
If you want something to log your loss, simply look at your reward ![]() that’s what your objective (negative loss) truly is.
that’s what your objective (negative loss) truly is.
I didn’t get it @vmoens , lets say we use vanilla loss, without subtraction of the b
for eg.
current_loss = -( reward * log(p(action)))
if reward == 0:
loss = 0
if reward == 1:
loss will be in range of [0.05, 1] if probablity is in range of [0.9, 0.1]
if reward == 2:
loss will be in range of [0.1, 2] if probablity is in range of [0.9, 0.1]
if reward == 3:
loss will be in range of [0.15, 3] if probablity is in range of [0.9, 0.1]
higher the reward higher the loss, lower the reward lower the loss.