Hi guys, long post incoming.
tl;dr PyTorch’s Adam has consistently worse performance for the exact same setting and by worse performance I mean PyTorch’s models cannot be used for this particular application.
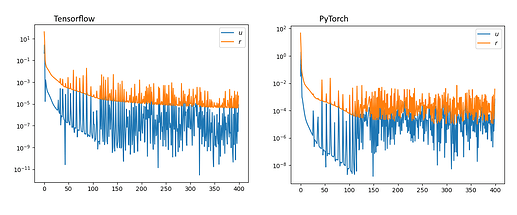
Probably similar to this and this
Okay first a bit of background:
I have implemented Raissi et al. ahttps://arxiv.org/abs/1711.10561(remove a in front of https, it is to get around the two links restriction) in both tf and pytorch.
The whole point is to get the network to approximate the solution to a PDE (1D Burger’s equation in this case). Both frameworks can approximate the solution but TF’s approximation is much better in that it can capture complex dynamics (i.e. the formation of a shock wave) while pytorch cannot meaning it probably cannot be used to solve more complex equations.
The results presented in the paper are reproducible in tf even when using a structure different from the original ahttps://github.com/maziarraissi/PINNs (remove a in front of https, it is to get around the two links restriction) implementation. My TF implementation is different from the original one but it is identical to the pytorch one for comparison.
TF works out of the box while in pytorch I could not replicate the results even when trying a whole lot of different configurations (network architectures, optimizers, etc…)
Now for the experiments:
I have tried to make the results as comparable as possible doing the following:
A:
- Same hyperparameters for Adam (default ones in TF)
- Same init (Xavier uniform)
When that didn’t work I went even further and:
B:
- Initialized weights in TF and loaded them in pytorch
- Initialized weights in pytorch and loaded them in TF
In A TF’s results are competitive while pytorch’s are not. In B it gets interesting because TF converges to a good result with its own weights but not with pytorch’s while pytorch doesn’t converge with neither its own nor with TF’s weights.
When doing a forward pass in pytorch/TF with the weights loaded from TF/pytorch they give the exact same answer so loading the weights is not the problem. Further, the fact the pytorch approximates the right solution somehow means the network is correctly wired.
This is a typical loss plot where TF is in blue and pytorch in orange.
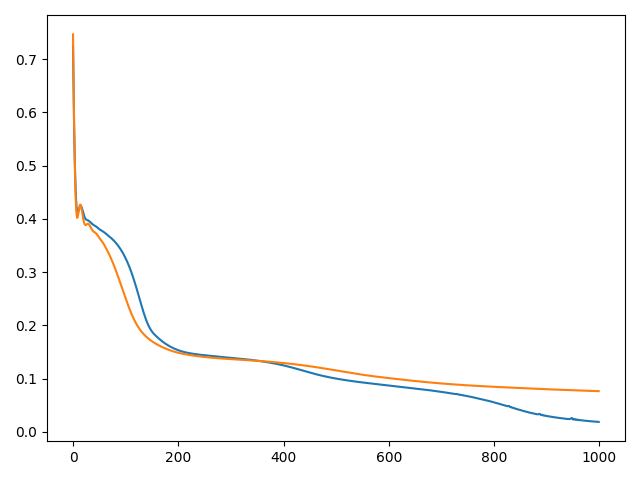
I can’t post more images because I’m a new user but in the plot of the solutions the TF solution approximates the discontinuity in the middle while pytorch can’t quite get there which makes me think it is an optimizer issue.
My ugly code for pytorch and TF below. Code is uncleaned but I’m here to clarify and discuss anything.
import numpy as np
import matplotlib.pyplot as plt
import torch
class PINN(torch.nn.Module):
def __init__(self):
super().__init__()
self.dim_real_in = 2
self.dim_img_in = 0
self.dim_real_out = 1
self.dim_img_out = 0
self.architecture = [20, 20, 20, 20]
self.activation_functions = ['tanh', 'tanh', 'tanh']
self.torch_activation = {'tanh': torch.tanh}
self.layers = self._get_layers()
self._initialize_weights()
def _get_layers(self):
self.architecture.insert(0, self.dim_real_in + self.dim_img_in)
l = []
print("Number of neurons and activation functions not equal. Using tanh for all")
for i in range(len(self.architecture) - 1):
layer = torch.nn.Linear(self.architecture[i], self.architecture[i + 1])
super().add_module("layer"+ str(i), layer)
l.append(layer)
l.append(self.torch_activation['tanh'])
layer = torch.nn.Linear(self.architecture[i + 1], self.dim_img_out + self.dim_real_out)
super().add_module("layer" + str(i + 1), layer)
l.append(layer)
return l
def _initialize_weights(self):
s = 0
for m in self.modules():
if isinstance(m, torch.nn.Linear):
# This bit loads weights from numpy arrays
# The loaded weights have identical forward passes as in TF!
# m.weight = torch.nn.Parameter(torch.from_numpy(np.load(str(s) + '_trained.npy')).T)
# s +=1
# m.bias = torch.nn.Parameter(torch.from_numpy(np.load(str(s) + '_trained.npy')))
# s +=1
torch.nn.init.xavier_uniform_(m.weight, gain=5/3)
torch.nn.init.constant_(m.bias, 0)
# This saves the weight init
# np.save(str(s) + '_torch.npy', m.weight.detach().numpy())
# s+=1
# np.save(str(s) + '_torch.npy', m.bias.detach().numpy())
# s+=1
def forward(self, t, x):
t.requires_grad = True
x.requires_grad = True
var = torch.cat((t, x), dim=1)
for l in self.layers:
var = l(var)
H = var
H_to_dif = H.sum()
dt, = torch.autograd.grad(H_to_dif, t, create_graph=True)
dx, = torch.autograd.grad(H_to_dif, x, create_graph=True)
dxx, = torch.autograd.grad(dx.sum(), x, retain_graph=True)
return H, dt, dx, dxx
class DataWrapper(torch.utils.data.Dataset):
def __init__(self, data, labels):
super().__init__()
self.data = data
self.labels = labels
def __getitem__(self, index):
return self.data[index], self.labels[index]
def __len__(self):
return self.data.shape[0]
class Schrodinger:
def __init__(self, targets):
self.model = self._build_model()
self.targets = targets
def _build_model(self):
model = PINN().to('cuda')
model = model.double()
print(model)
return model
def physics(self,t ,x):
u, u_t, u_x, u_xx = self.model.forward(t, x)
f = u_t + u * u_x - 0.01 * u_xx
return f, u
def loss(self, t, x, labels):
initial_mask = (t[:,0] == 0)
boundary_mask = ((x[:,0] == -1) | (x[:,0] == 1)) & (t[:,0] != 0)
structure_mask = ~ (initial_mask | boundary_mask)
f, u = self.physics(t, x)
l = torch.zeros_like(u)
structure_norm = structure_mask.sum()
boundary_norm = boundary_mask.sum()
initial_norm = initial_mask.sum()
l[structure_mask] = f[structure_mask]
l[boundary_mask] = u[boundary_mask]
l[initial_mask] = u[initial_mask]
labels = labels.reshape(-1,1)
l = (l - labels)**2
l[structure_mask] = l[structure_mask] /structure_norm
l[boundary_mask] = l[boundary_mask] / boundary_norm
l[initial_mask] = l[initial_mask] / initial_norm
self.structure_loss = [l[structure_mask].sum(), structure_norm]
self.boundary_loss = [l[boundary_mask].sum(), boundary_norm]
self.initial_loss = [l[initial_mask].sum(), initial_norm]
l = l.sum()
return l
def train(self, t, x, epochs):
self.loss_histogram = []
self.weight_histogram = []
optimizer = torch.optim.Adam(self.model.parameters(),
lr=1e-3, eps=1e-07, weight_decay=0, amsgrad=False)
# optimizer = torch.optim.LBFGS(self.model.parameters(), lr=0.1)
# scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=1000, gamma=0.9)
print("Training params: ", len(list(self.model.parameters())))
for i in range(epochs):
w = 0
self.prt = True
optimizer.zero_grad()
def closure():
self.model.zero_grad()
loss = self.loss(t, x, self.targets[:, 2])
loss.backward()
self.loss_histogram.append(loss.item())
if i % 100 == 0 and self.prt:
self.prt = False
print("Epoch: {:1.0f}, loss: {:1.5f} ".format(i,
loss.item()))
print("struc: {:1.5f}, n: {:1.0f}, bdry: {:1.5f}, n: {:1.0f}, initial: {:1.5f}, n: {:1.0f}".format(
self.structure_loss[0].item(), self.structure_loss[1].item(),
self.boundary_loss[0].item(), self.boundary_loss[1].item(),
self.initial_loss[0].item(), self.initial_loss[1].item()))
return loss
optimizer.step(closure)
# scheduler.step()
for m in self.model.modules():
if isinstance(m, torch.nn.Linear):
w += (m.weight**2).sum()
self.weight_histogram.append(w)
plt.plot(self.loss_histogram)
plt.show()
np.savetxt('pytorch.txt', self.loss_histogram)
plt.plot(self.weight_histogram)
plt.show()
if __name__ == "__main__":
from itertools import product
torch.set_printoptions(precision=10)
shape_x = 200
shape_t = 200
X = np.linspace(-1, 1, shape_x)
T = np.linspace(0, 1, shape_t)
Z = np.zeros(shape_t*shape_x)
prod = product(T, X)
prod = np.array(list(prod))
prod = np.insert(prod, 2 ,0, axis=1)
sin_form = - np.sin(np.pi*X)
prod[prod[:,0] == 0, 2] = sin_form
prod[(prod[:,0] == -1) | (prod[:,0] == 1), 2] = 0
x_coord, t_coord = [], []
for t, x, z in prod:
x_coord.append(x)
t_coord.append(t)
X = np.array(x_coord).reshape(-1, 1)
T = np.array(t_coord).reshape(-1, 1)
dtype = torch.float64
X_tensor = torch.tensor(X, dtype=dtype).to('cuda')
T_tensor = torch.tensor(T, dtype=dtype).to('cuda')
total_data = torch.tensor(prod, dtype=dtype).to('cuda')
point_t = torch.tensor([[2]], dtype=dtype).to('cuda')
point_x = torch.tensor([[2]], dtype=dtype).to('cuda')
model = Schrodinger(total_data)
model.train(T_tensor, X_tensor, 1000)
out, _ , _, _ = model.model.forward(T_tensor, X_tensor)
# Compare forward with forward from TF. If using same weights error = 0
# out_tf = np.load('output_tf.npy')
# error = (out.detach().cpu() - out_tf)**2
# error = error.sum()
# print(error)
im = out.reshape(shape_t, shape_x).detach().cpu().T
for i in range(0, im.shape[1], 50):
plt.plot(prod[prod[:,0] == 0,1], im[:, i])
plt.show()
plt.imshow(out.detach().cpu().reshape(shape_t,shape_x).T)
plt.show()
import numpy as np
import tensorflow as tf
import itertools
import matplotlib.pyplot as plt
tf.disable_v2_behavior()
class PINN:
def __init__(self, layers, f_x, g_t, alpha):
self.initial_condition = f_x
self.boundary_condition = g_t
self.layers = layers
self.alpha = alpha
self.x = tf.placeholder(tf.float64, shape=[None, 1])
self.t = tf.placeholder(tf.float64, shape=[None, 1])
self.num_points_space = 200
self.num_points_time = 200
def mlp(self, t, x, variable_scope='default'):
output = tf.concat([t, x], axis=1)
# Pass through MLP
with tf.variable_scope(variable_scope, reuse=tf.AUTO_REUSE):
for i, size in enumerate(self.layers):
output = tf.nn.tanh(tf.layers.dense(output, size, name="layer_{}".format(i)))
# Last layer without a tanh
output = tf.layers.dense(output, 1, name="layer_{}".format(i + 1))
return output
def gen_data(self):
X = np.linspace(-1, 1, self.num_points_space)
T = np.linspace(0, 1, self.num_points_time)
prod = itertools.product(T, X)
x_coord, t_coord = [], []
for t, x in prod:
x_coord.append(x)
t_coord.append(t)
X = np.array(x_coord).reshape(-1, 1)
T = np.array(t_coord).reshape(-1, 1)
return T, X
def PDE_constraint(self, t, x):
u = self.mlp(t, x)
u_t = tf.gradients(u, t, unconnected_gradients='zero')[0]
u_x = tf.gradients(u, x, unconnected_gradients='zero')[0]
u_xx = tf.gradients(u_x, x, unconnected_gradients='zero')[0]
f = u_t + u*u_x - self.alpha*u_xx
return f
def loss(self, t, x):
L_f = tf.square(self.PDE_constraint(t, x)) #- self.poisson_condition(t, x))
L_u_time = tf.square(self.mlp(t, x) - self.boundary_condition(t))
L_u_space = tf.square(self.mlp(t, x) - self.initial_condition(x))
cond = ~tf.equal(t, 0) & ~tf.equal(x, 1) & ~tf.equal(x, -1)
normalization_f = tf.reduce_sum(tf.cast(cond, tf.float64))
L_f = tf.where(cond, L_f, tf.zeros_like(L_f))
cond = (tf.equal(x, 1) | tf.equal(x, -1)) & ~tf.equal(t, 0)
normalization_u_time = tf.reduce_sum(tf.cast(cond, tf.float64))
L_u_time = tf.where(cond, L_u_time, tf.zeros_like(L_u_time))
cond = tf.equal(t, 0)
normalization_u_space = tf.reduce_sum(tf.cast(cond, tf.float64))
L_u_space = tf.where(cond, L_u_space, tf.zeros_like(L_u_space))
return tf.reduce_sum(L_f)/normalization_f + \
tf.reduce_sum(L_u_space)/normalization_u_space + \
tf.reduce_sum(L_u_time)/normalization_u_time
def detailed_loss(self, t, x):
L_f = tf.square(self.PDE_constraint(t, x)) #- self.poisson_condition(t, x))
L_u_time = tf.square(self.mlp(t, x) - self.boundary_condition(t))
L_u_space = tf.square(self.mlp(t, x) - self.initial_condition(x))
cond = ~tf.equal(t, 0) & ~tf.equal(x, 1) & ~tf.equal(x, -1)
normalization_f = tf.reduce_sum(tf.cast(cond, tf.float64))
L_f = tf.where(cond, L_f, tf.zeros_like(L_f))
cond = (tf.equal(x, 1) | tf.equal(x, -1)) & ~tf.equal(t, 0)
normalization_u_time = tf.reduce_sum(tf.cast(cond, tf.float64))
L_u_time = tf.where(cond, L_u_time, tf.zeros_like(L_u_time))
cond = tf.equal(t, 0)
normalization_u_space = tf.reduce_sum(tf.cast(cond, tf.float64))
L_u_space = tf.where(cond, L_u_space, tf.zeros_like(L_u_space))
return tf.reduce_sum(L_f)/normalization_f, \
tf.reduce_sum(L_u_space)/normalization_u_space, \
tf.reduce_sum(L_u_time)/normalization_u_time, \
normalization_f, normalization_u_space, normalization_u_time
def train(self, training_iter):
plot_loss = []
T, X = self.gen_data()
loss = self.loss(self.t, self.x)
tf_dict = {self.t: T, self.x: X}
optimizer_Adam = tf.train.AdamOptimizer()
train_op_Adam = optimizer_Adam.minimize(loss)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
# Code below loads weight inits
# s = 0
# for v in tf.trainable_variables():
# w = np.load(str(s) + '_torch.npy').T
# sess.run(v.assign(w))
# # print(sess.run(v))
# s += 1
# Code below saves weight inits
# for v in tf.trainable_variables():
# np.save(str(s), sess.run(v))
# s += 1
# Saves the forward pass to compare it with pytorch's
# im = sess.run(self.mlp(T, X))
# np.save('output_tf.npy', im)
# im = np.load('output_tf.npy').reshape(self.num_points_space, self.num_points_time)
# plt.imshow(im.T)
# plt.show()
for it in range(training_iter):
print(it)
_, l = sess.run([train_op_Adam, loss], tf_dict)
plot_loss.append(l)
plt.plot(plot_loss)
np.savetxt('tf.txt', plot_loss)
print("TOTAL LOSS: ", l)
plt.show()
data1 = sess.run(self.mlp(X[T == 0, np.newaxis], T[T == 0, np.newaxis]))
data2 = sess.run(self.mlp(X[T == 0.5, np.newaxis], T[T == 0.5, np.newaxis]))
data3 = sess.run(self.mlp(X[T == 1, np.newaxis], T[T == 1, np.newaxis]))
self.plot(data1, data2, data3)
total_f = sess.run(self.PDE_constraint(self.x, self.t), tf_dict)
L_f, L_space, L_time, normalization_f, normalization_u_space, normalization_u_time = sess.run(self.detailed_loss(self.x, self.t), tf_dict)
print("TOTAL PDE constraint violation: ", np.sum(np.square(total_f)))
print("TOTAL f constraint violation: ", L_f)
print("TOTAL time constraint violation: ", L_time)
print("TOTAL space constraint violation: ", L_space)
print("NUMBER f constraint violation: ", normalization_f)
print("NUMBER time constraint violation: ", normalization_u_time)
print("NUMBER space constraint violation: ", normalization_u_space)
im = sess.run(self.mlp(T, X)).reshape(self.num_points_space, self.num_points_time)
plt.imshow(im.T)
plt.show()
s = 0
for v in tf.trainable_variables():
np.save(str(s) + "_trained", sess.run(v))
s += 1
return sess
def predict(self,sess, t, x, shape_x, shape_t):
pred = sess.run(self.mlp(t, x))
im = pred.reshape(shape_x, shape_t).T
for i in range(0, im.shape[1], 50):
plt.plot(im[:, i])
plt.show()
plt.imshow(im)
plt.show()
def plot(self, data1, data2, data3):
plt.plot(data1)
plt.plot(data2)
plt.plot(data3)
plt.show()
def zero(t):
return tf.zeros_like(t)
def shifted_sin(x):
return -tf.sin(np.pi * x)
if __name__ == "__main__":
shape_x = 500
shape_t = 500
X = np.linspace(-1, 1, shape_x)
T = np.linspace(0, 1, shape_t)
prod = itertools.product(T, X)
x_coord, t_coord = [], []
for t, x in prod:
x_coord.append(x)
t_coord.append(t)
X = np.array(x_coord).reshape(-1, 1)
T = np.array(t_coord).reshape(-1, 1)
architecture = [20, 20, 20, 20]
PINN = PINN(architecture, shifted_sin, zero, alpha=0.01)
sess = PINN.train(1000)
PINN.predict(sess, T, X, shape_x, shape_t)
sess.close()